The other part of the question is this:Since the function f(a) is (options- continuous, not necessarily continuous, or not continuous) on its domain, the intermediate value theorem (options- can be applied or cannot be applied) (Options for can be applied down below)and states that for any value kin the intervalthere exists a value c, where (blank)

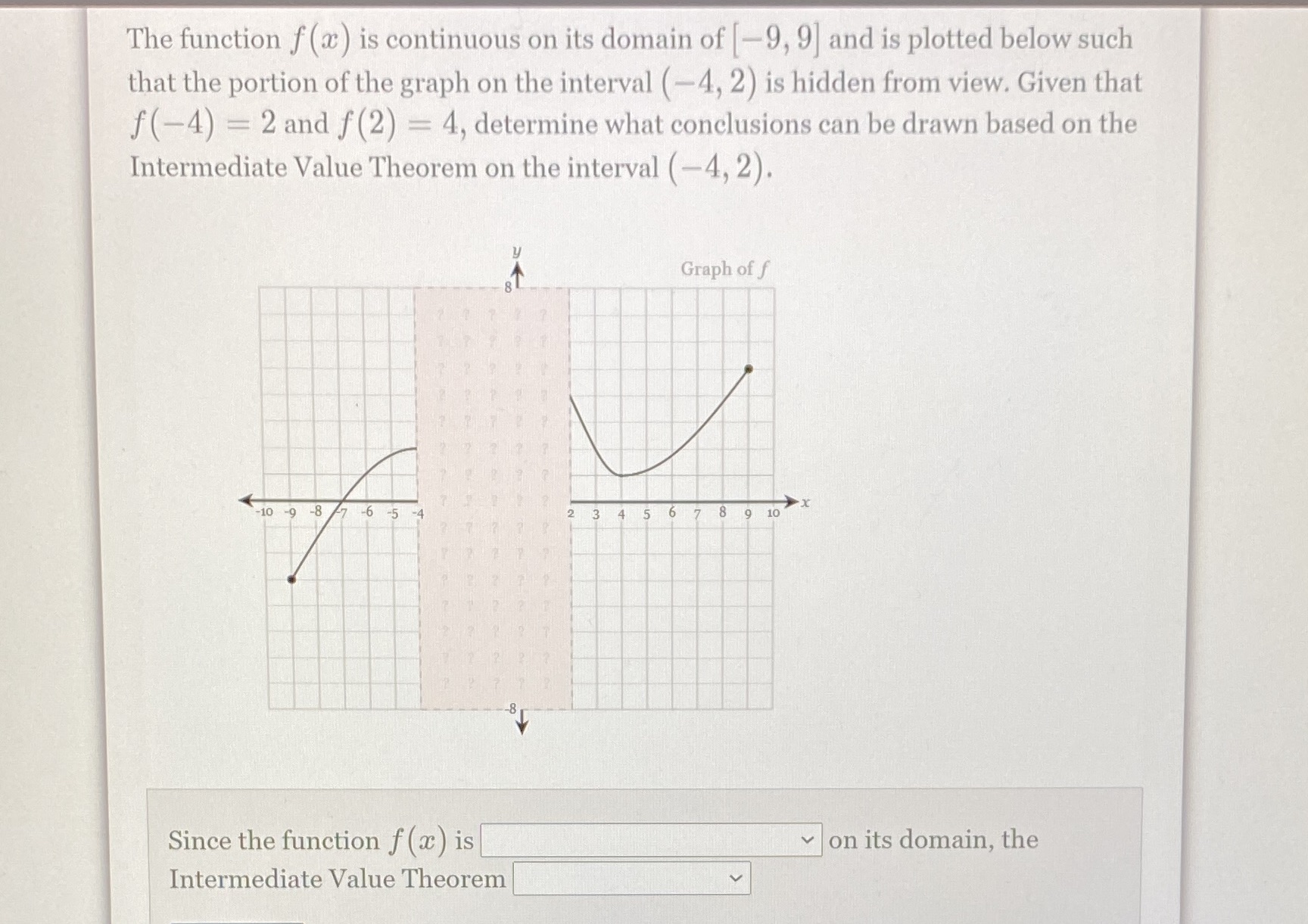
The function f (x ) is continuous on its domain of [-9, 9] and is plotted below such that the portion of the graph on the interval (-4, 2) is hidden from view. Given that f(-4) = 2 and f(2) = 4, determine what conclusions can be drawn based on the Intermediate Value Theorem on the interval (-4, 2). Graph of f -10 -9 -8 7 6 -5 3 4 5 6 7 8 9 10 Since the function f (x) is on its domain, the Intermediate Value Theorem v