Question: The Standard Deviation for Stocks = 18.63 and the Standard Deviation for Bonds = 8.27. Define Correlation coefficient and what it represents in a two-security
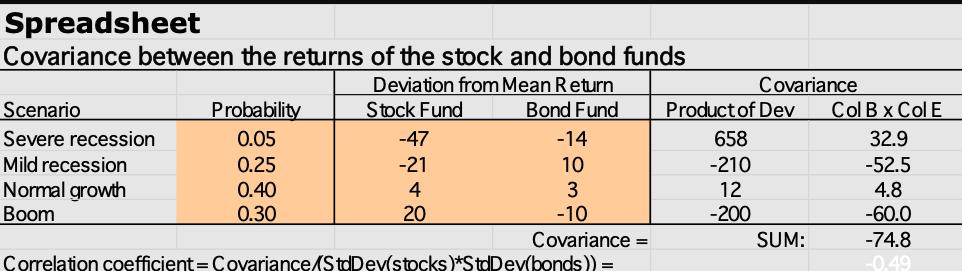
The Standard Deviation for Stocks = 18.63 and the Standard Deviation for Bonds = 8.27.
- Define Correlation coefficient and what it represents in a two-security portfolio.
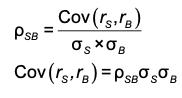
- Calculate the correlation coefficient for the above asset allocation.
- At what level do we have perfect negative correlation and what would that mean?
- At what level do we achieve perfect positive correlation and why would we avoid this for diversification purposes?
- According to Bodie Kane and Marcus, what would be an acceptable level of negative correlation for the effective diversification of a portfolio?
- What does the image below illustrate?
- Why would we want to gauge diversification in this manner?
Spreadsheet Covariance between the returns of the stock and bond funds Deviation from Mean Return Stock Fund Bond Fund Scenario Severe recession Mild recession Normal growth Boom Probability 0.05 0.25 0.40 0.30 -47 -21 4 20 -14 10 3 -10 Covariance = Correlation coefficient = Covariance/StdDev(stocks)*StdDev(bonds)) = Covariance Product of Dev 658 -210 12 -200 SUM: Col B x Col E 32.9 -52.5 4.8 -60.0 -74.8 -0.49
Step by Step Solution
3.33 Rating (153 Votes )
There are 3 Steps involved in it
Question your portfolio and manage risks Anscucr cors cloution c... View full answer

Get step-by-step solutions from verified subject matter experts


