This is a Linear Algebra Question. BOTH the question and the answer are shown below.

I have been able to complete all of the first question, but I do not understand the answer given for extending Lin={v?, v?} as a basis.

In particular, I do not understand how x+y-z=0 was obtained, since I assumed x+y+z=0.

Please explain this ?

I understand, that once n is obtained that normalisation occurs as u? = n/||n||, thus the extended orthonormal basis is {u?, u?, u?}, and therefore I understand how 1/?3 is obtained, so no need to explain this.

QUESTION

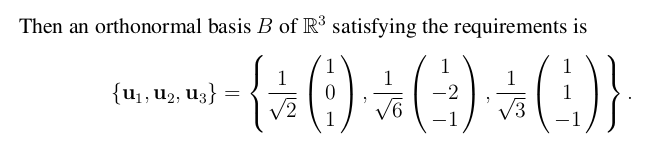
Problem 10.7 Show that S = {v,, v2, val is a basis of p3, where 2 V1 O V2 - V3 = Beginning with the vector v, find an orthonormal basis of the subspace Lin(V1, v21. Using any method, extend this to an orthonormal basis B of JP3.\fProblem 10.7 Write the vectors as the columns of a matrix Ps and then evaluate PS : Ps |Ps| = -3 0. Therefore S is a basis of RS. To find an orthonormal basis of the subspace Lin { v1, v2}, let u1 = v1. Then set W A vector parallel to w is w = (1, -2, -1). Check that w _ uj. (You can also check that w E Lin {v1, v2} by showing that it is a linear combination of v1 and V2.) Then { u1, u2} - I've ( ! ) io ( : is an orthonormal basis of Lin{ v1, V2}. (Another possible choice is { ul, -u2}.) You can extend this to a basis of IR3 either by applying the Gram-Schmidt process again using any vector which is not in Lin {v1, v2}, such as v3, or you can find the Cartesian equation of the plane Lin { V1, V2} and use the normal vector. For example, we have rty - 2=0. so that n =