This is a practice exmaple problem we got for practice I do not know how to start or solve it$,$ can you solve showing all steps and explain them.

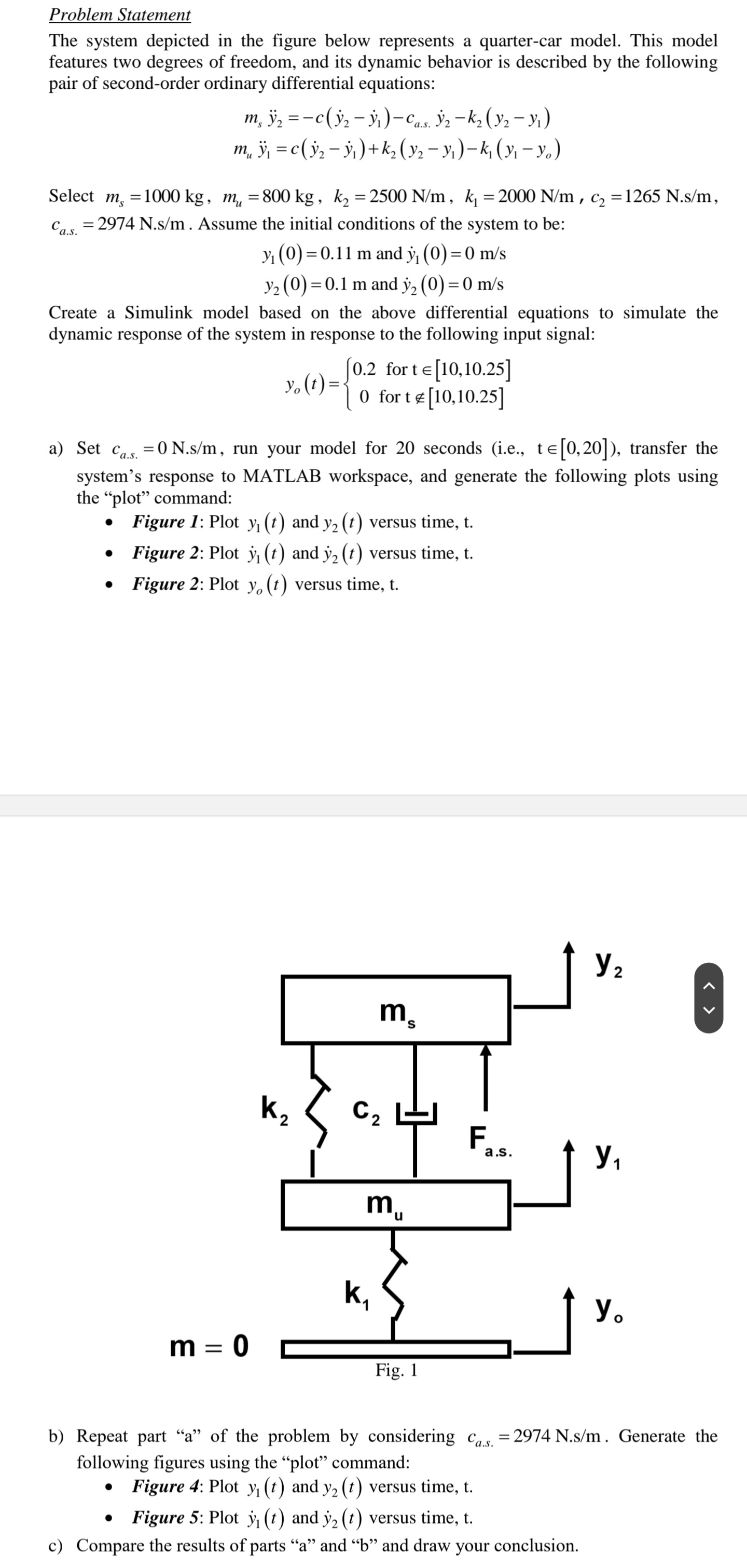
Problem Statement

The system depicted in the figure below represents a quarter$-$car model. This model

features two degrees of freedom, and its dynamic behavior is described by the following

pair of second$-$order ordinary differential equations:

$m_s{y}_2^{}=-c(y_2^{}-y_1^{})-c_{a.s.}{y}_2^{}-k_2(y_2-y_1)$

$m_u{y}_1^{}=c(y_2^{}-y_1^{})+k_2(y_2-y_1)-k_1(y_1-y_o)$

Select $m_s=1000kg,m_u=800kg,k_2=2500\frac{N}{m},k_1=2000\frac{N}{m},c_2=1265N.\frac{s}{m},$

$c_{a.s.}=2974N.\frac{s}{m}.$ Assume the initial conditions of the system to be:

$y_1(0)=0\mathrm{.}11m$ and $y_1^{}(0)=0\frac{m}{s}$

$y_2(0)=0\mathrm{.}1m$ and $y_2^{}(0)=0\frac{m}{s}$

Create a Simulink model based on the above differential equations to simulate the

dynamic response of the system in response to the following input signal:

$y_o(t)=\{\begin{array}{ccc}0\mathrm{.}2& \text{f}\text{o}\text{r}\text{t}\text{i}\text{n}[10,& 10\mathrm{.}25]\\ 0& \text{f}\text{o}\text{r}t!in[10,& 10\mathrm{.}25]\end{array}$

a$)$ Set $c_{a.s.}=0N.\frac{s}{m},$ run your model for $20$ seconds $($i$.$e$.,$ tin$[0,20]),$ transfer the

system's response to MATLAB workspace, and generate the following plots using

the "plot" command:

Figure $1$: Plot $y_1(t)$ and $y_2(t)$ versus time, t $.$

Figure $2$: Plot $y_1^{}(t)$ and $y_2^{}(t)$ versus time, t $.$

Figure $2$: Plot $y_o(t)$ versus time, t $.$

b$)$ Repeat part $"$ a $"$ of the problem by considering $c_{a.s.}=2974N.\frac{s}{m}.$ Generate the

following figures using the "plot" command:

Figure $4$: Plot $y_1(t)$ and $y_2(t)$ versus time, t $.$

Figure $5$: Plot $y_1^{}(t)$ and $y_2^{}(t)$ versus time, t $.$

c$)$ Compare the results of parts $"$a$"$ and $"$b$"$ and draw your conclusion.