this question simplex tablue method please

here how we took in class and thanks alot

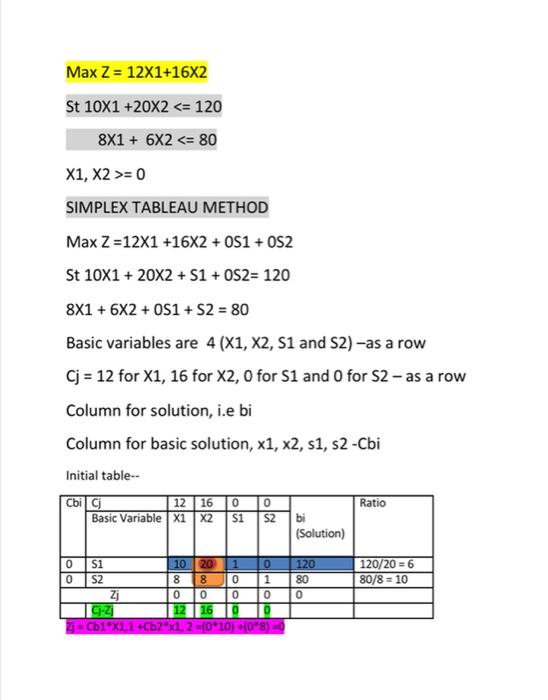
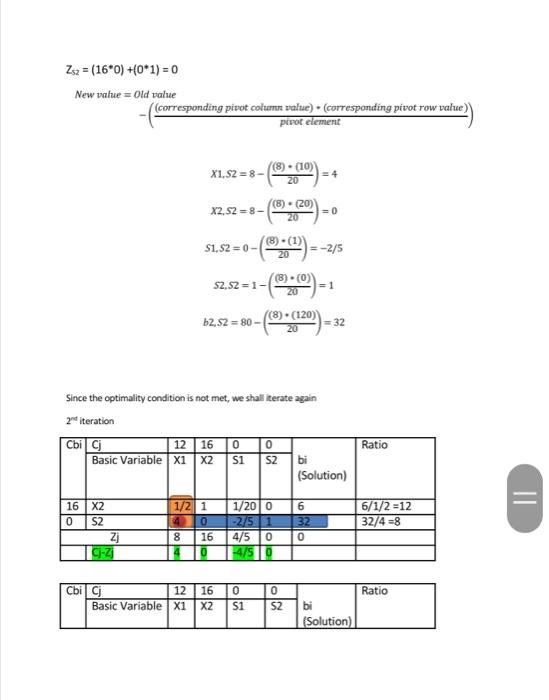
Assume that in the context of a production problem there are two products, P and P that are manufactured on three machines, M1, M2, and M3. Each product has to be processed on each of the three machines, but the order in which the products are processed on the machines is assumed to be immaterial. The two products sell for the (fixed) unit price of $12 and $27, respectively, while the capacities of the three machines are 15, 14, and 12 hours, respectively. Note that the capacities are expressed for the planning period, e.g., one day, It is important that all other capacity uses are then also expressed in the same units for the same planning period. The different capacities may result from different expected maintenance requirements. Now, 9 minutes is required to process one unit of unit of P, on M, 6 minutes to process one unit of P on M2, and 10 minutes to process one unit of P, on M3. The corresponding data for P2 are 12, 14, and 18. Finally, it is required that at least 70 product units are made and sold. Max Z = 12X1+16X2 St 10X1 +20X2 = 0 SIMPLEX TABLEAU METHOD Max 2 =12X1 +16X2 +0S1 + S2 St 10X1 + 20X2 +51 + OS2= 120 8X1 + 6X2 +0S1 + S2 = 80 Basic variables are 4 (X1, X2, S1 and S2) -as a row Cj = 12 for X1, 16 for X2,0 for S1 and 0 for S2 - as a row Column for solution, i.e bi Column for basic solution, x1, x2, s1, s2 -Cbi Initial table- Cbi C 12 16 0 0 Ratio Basic Variable x1 X2 51 52 (Solution) bi 0 S1 1020 1 0 0 S2 8 80 1 Zj 0 0 0 0 Cj-2 12 16 0 D 2i = Cb1*X1.1 +Cb2"x1,2 = 010) +(098) =0 120 80 0 120/20 = 6 80/8 = 10 Gj Column 1 = 12-0 = 12 Pivot element = 20, then 51 is leaving variable and X2 is entering variable Check for the optimality conditions For maximization problems G-Z) =0, that it can only have 0 or positive values For the problem at hand, the optimality condition is not met. Therefore we shall continue to iterate the simplex tableau algorithm 1.. determine the pivot element by finding the pivot row and column, pivot element = 20 First iteration 12 16 0 Basic Variable x1 X2 Ratio $1 S2 bi (Solution) 4 0 1/200 -2/51 4/50 4/50 6 32 0 16 X2 1/2 L 0 S2 Z; 8 16 C-2) 4 10 Zx1 = (16*1/2) +(0*4) = 8 Zo = (16*1) +(0*0) = 16 Zs: = (16*1/20) +(0-1) 4/5 Z2 = (16*0) +(0*1) = 0 New value = Old value corresponding pivot column value). corresponding pivot row value perot element X1.S2 = 8- (8) . (10) = 4 20 X2,928- (8) - (20 20 = 0 S1, S2 = 0 - (8) -(1) 20 =-2/5 SZ, S2 = 1 (8) -(0) = 1 20 62,52 = 80 - (8) . (120) = 32 Since the optimality condition is not met, we shall iterate again 24 iteration Cbij 12 16 0 0 Basic Variable X1 X2 si S2 bi (Solution) Ratio 6/1/2 =12 32/4 =8 = 16 X2 0 S2 Z] C-2 1/2 1 4 10 8 16 4 10 1/2010 -2/51 4/5 0 -4/50 6 32 0 Cbici 12 16 0 Basic Variable X1 X2 51 S2 Ratio bi (Solution) 16 X2 0 1 1/10 1/8 2 12 X1 10 -1/10 1/48 zj 12 16 2/5 1 128 C:21 12/511 S2 will be leaving the tableau while X1 will be entering the basic solution 0 (1/2) (0) = 1 x1.x2 = 12-(0/2) = 6) = 0 X2, X2 = 1 - - (43)*(?). (C) (1) S1,x2 = 1/20 - - 1/10 X2.52 = 0 - -1/8 b2, X2-6- -(4/2) = 82) - (() = 2