Question: Value a three-year option-free zero-coupon bond using binomial interest rate tree. Value a four-year option-free zero-coupon bond using binomial interest rate tree. Value a four-year
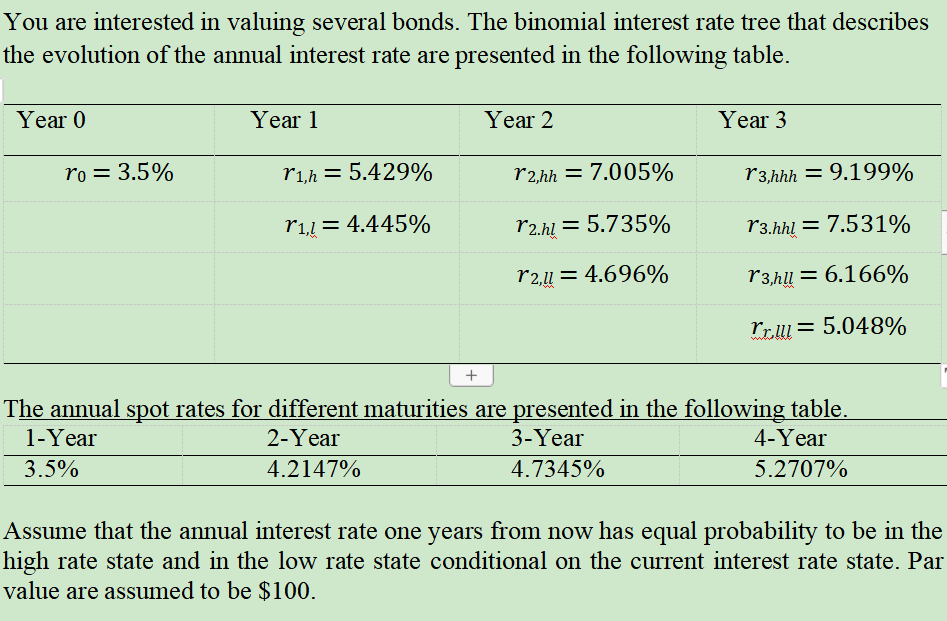
- Value a three-year option-free zero-coupon bond using binomial interest rate tree.
- Value a four-year option-free zero-coupon bond using binomial interest rate tree.
- Value a four-year option-free bond that pays 6.5% coupon annually using binomial interest rate tree.
- Value the same bond in question 3 using spot rates.
- Value a four-year callable bond that pays 6.5% coupon annually using binomial interest rate tree. The bond is callable on each coupon payment date, and the call price is $100.
- What is the value of the call option embedded in the above callable bond?
- Value a four-year callable bond that pays 6.5% coupon annually using binomial interest rate tree. The bond is callable at the end of second and third years, and the call price is $100.
You are interested in valuing several bonds. The binomial interest rate tree that describes the evolution of the annual interest rate are presented in the following table. Year 0 Year 1 Year 2 2 Year 3 ro =3.5% r1h = 5.429% r 2 hh = 7.005% r 3,hhh = 9.199% r 1,1 = 4.445% r2.hl = 5.735% r3.hhl = 7.531% r2,u = 4.696% r3,hu = 6.166% Prlu = 5.048% + The annual spot rates for different maturities are presented in the following table. 1-Year 2-Year 3-Year 4-Year 3.5% 4.2147% 4.7345% 5.2707% Assume that the annual interest rate one years from now has equal probability to be in the high rate state and in the low rate state conditional on the current interest rate state. Par value are assumed to be $100
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


