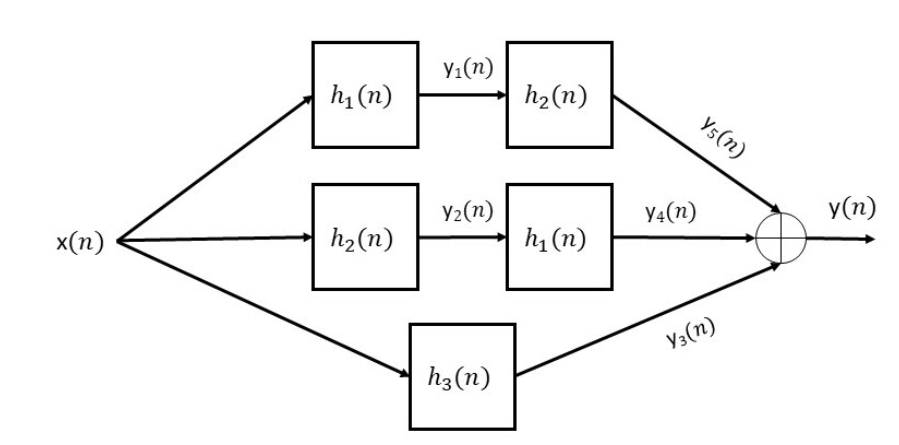
with hi(n) as the impulse response for the system y1(n) + 0.5y1(n-1) = x(n) and 2(n) as the impulse response for the system y2(n) - 0.5y2 (n-1)= x(n) and hg(n) as the impulse response for the system y3 (n) +0.5y3 (n-2) = x(n) 1. Use MATLAB step signal function from Module 5 to generate x(n), a pulse from n=0 to n-50 samples. 2. Find H(z) for all three systems from the three difference equations. 3. Use MATLAB to check the stability of the three systems. 4. Use MATLAB and the transfer functions you obtained in part 2 and the filter function (with the impulse signal MATLAB function from Module 5) to find h(n) through h3 (n). 5. Use MATLAB to generate y(n) through yg(n) (do not use convolution). 6. Plot all signals in the figure given above and label them properly. x(n) h (n) h (n) Y(n) Y(n) h(n) h (n) h (n) Y4(n) Y5 (n) Y3(n) y(n)