The digital system shown in figure uses a six-bit (including sign) fixed-point two?s-complement A/D converter with rounding, and the filter H(z) id implemented using eight-bit (including sign) fixed-point two?s-complement fractional arithmetic with rounding. The input x(t) is zero-mean uniformly distributed random process having autocorrelation y_zz(t) = 3?(r). Assume that the A/D converter can handle input values up to ?1.0 without overflow.

(a) What value of attention should be applied prior to the A/D converter to assure that it does not overflow?

(b) With the attenuation above, what is the signal-to-quantization noise ratio (SNR) at the A/D converter output?

(c) The six-bit A/D samples can be left-justified, right-justified, or centered in the eight-bit word used as the input to the digital filter. What is the correct strategy to use for maximum SNR at the filter output without overflow?

(d) What is the SNR at the output of the filter due to all quantization noise sources?

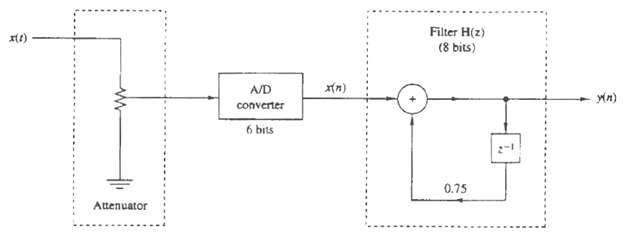
Filter H(z) (8 bits) ) A/D converter 6 bits 0.75 Attenuator