With regards to the three-asset optimization in the attached Excel spreadsheet (Test2-student), find the optimal allocations for stocks, bonds, and real estate based on the portfolio returns, standard deviations, and correlations provided in the Inputs Table in order to:

1. Obtain a 3% target return per period.

2. Obtain the same 3% target return per period assuming the correlation between stocks and real estate is -0.15 (changed from 0.15).

3. Obtain a 2.5% target return per period assuming the correlation between stocks and real estate remains at -0.15.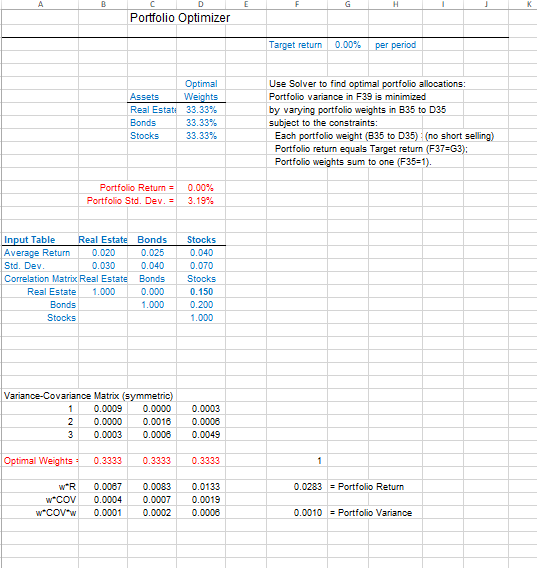

A F Portfolio Optimizer Target return 0.00% per period Optimal Assets Weights Real Estate 33.33% Bonds 33.33% Stocks 33.33% Use Solver to find optimal portfolio allocations: Portfolio variance in F39 is minimized by varying portfolio weights in B35 to D35 subject to the constraints: Each portfolio weight (B35 to D35) (no short selling) Portfolio return equals Target return (F37=G3): Portfolio weights sum to one (F35=1). Portfolio Return = Portfolio Std. Dev. = 0.00% 3.19% Input Table Real Estate Bonds Average Return 0.020 0.025 Std. Dev. 0.030 0.040 Correlation Matrix Real Estate Bonds Real Estate 1.000 0.000 Bonds 1.000 Stocks Stocks 0.040 0.070 Stocks 0.150 0.200 1.000 Variance-Covariance Matrix (symmetric) 1 0.0009 0.0000 2 0.0000 0.0018 3 0.0003 0.0006 0.0003 0.0008 0.0049 Optimal Weights 0.3333 0.3333 0.3333 1 0.0283 = Portfolio Return WER w*COV wCOVw 0.0067 0.0004 0.0001 0.0083 0.0007 0.0002 0.0133 0.0019 0.0006 0.0010 - Portfolio Variance A F Portfolio Optimizer Target return 0.00% per period Optimal Assets Weights Real Estate 33.33% Bonds 33.33% Stocks 33.33% Use Solver to find optimal portfolio allocations: Portfolio variance in F39 is minimized by varying portfolio weights in B35 to D35 subject to the constraints: Each portfolio weight (B35 to D35) (no short selling) Portfolio return equals Target return (F37=G3): Portfolio weights sum to one (F35=1). Portfolio Return = Portfolio Std. Dev. = 0.00% 3.19% Input Table Real Estate Bonds Average Return 0.020 0.025 Std. Dev. 0.030 0.040 Correlation Matrix Real Estate Bonds Real Estate 1.000 0.000 Bonds 1.000 Stocks Stocks 0.040 0.070 Stocks 0.150 0.200 1.000 Variance-Covariance Matrix (symmetric) 1 0.0009 0.0000 2 0.0000 0.0018 3 0.0003 0.0006 0.0003 0.0008 0.0049 Optimal Weights 0.3333 0.3333 0.3333 1 0.0283 = Portfolio Return WER w*COV wCOVw 0.0067 0.0004 0.0001 0.0083 0.0007 0.0002 0.0133 0.0019 0.0006 0.0010 - Portfolio Variance