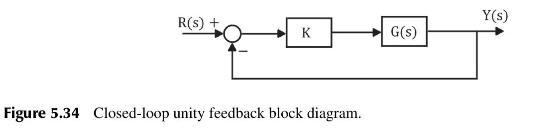
Question: Consider a general closed-loop unity feedback control system shown in Figure 5.34, where (K) is the controller gain and (G(s)) is the plant Transfer Function
Consider a general closed-loop unity feedback control system shown in Figure 5.34, where \(K\) is the controller gain and \(G(s)\) is the plant Transfer Function model.
(a) For the two systems with the following plant Transfer Function models
\[\begin{aligned}G(s) & =\frac{3 s-4}{s^{2}-2 s+2} \\G(s) & =-\frac{3 s-4}{s^{2}-2 s+2} .\end{aligned}\]
(i) Obtain the root loci for the two systems.
(ii) Is there any value of controller gain \(K\) that will stabilise either of these plants?
(b) Sketch the root loci for the dynamic systems with the following plant Transfer Function models:
(i) \(G(s)=\frac{(s+2)(s+6)}{s^{2}+8 s+25}\)
(ii) \(G(s)=\frac{s^{2}+4}{s^{2}+1}\)
(iii) \(G(s)=\frac{s^{2}+1}{s^{2}}\)
(iv) \(G(s)=\frac{1}{(s+1)^{3}(s+4)}\).
R(s) + Y(s) K G(s) Figure 5.34 Closed-loop unity feedback block diagram.
Step by Step Solution
3.29 Rating (155 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


