Consider the matrix equation ([mathbf{A}]{mathbf{x}}={mathbf{b}}) given by a. Construct the quadratic form (F(mathbf{x})={mathbf{x}}^{mathrm{T}}[mathbf{A}]{mathbf{x}}-2{mathbf{x}}^{mathrm{T}}{mathbf{b}}). b. Find ({mathbf{x}}=left{mathbf{x}^{*} ight}) by minimizing (F(mathbf{x})). c. Verify that the vector

Consider the matrix equation \([\mathbf{A}]\{\mathbf{x}\}=\{\mathbf{b}\}\) given by

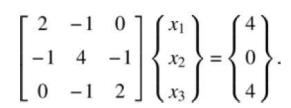
a. Construct the quadratic form \(F(\mathbf{x})=\{\mathbf{x}\}^{\mathrm{T}}[\mathbf{A}]\{\mathbf{x}\}-2\{\mathbf{x}\}^{\mathrm{T}}\{\mathbf{b}\}\).

b. Find \(\{\mathbf{x}\}=\left\{\mathbf{x}^{*}\right\}\) by minimizing \(F(\mathbf{x})\).

c. Verify that the vector \(\left\{\mathbf{x}^{*}\right\}\) satisfies \([\mathbf{A}]\{\mathbf{x}\}=\{\mathbf{b}\}\).

2-10 -1 4-1 0-12 18-8 X3 0 4