For the 4node plane strain finite element, finite element computation yields the displacements at the nodes as follows: \(\left\{u_{1}, v_{1}, u_{2}, v_{2}, u_{3}, v_{3}, u_{4}, v_{4}\right\}=\{-1,0,-1,0,0,1,0\), \(1\} \times 10^{-4}\). The connectivity table is as shown in the table.

The local and global node numbering are shown in the physical and parametric spaces, respectively, in the figure above.

a. Where is the point \((s, t)=(0.0,0.0)\), located in the global \((x, y)\) coordinates?

b. Determine the Jacobian matrix for this element.

c. Find the derivate of \(u\) with respect to \(x\) and \(y,(\partial u / \partial x, \partial u / \partial y)\) at the centroid.

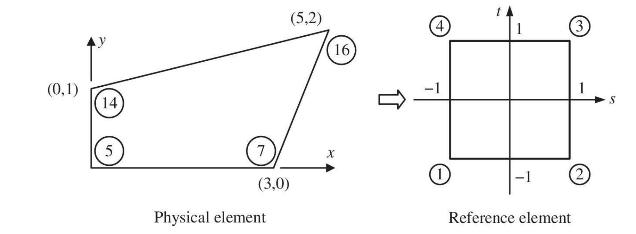
Element Local node 1 Local node 2 Local node 3 Local node 4 i 5 7 16 14