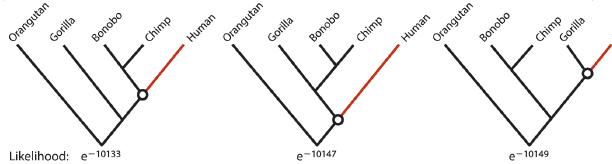
Phylogenetic trees like those in Figure 20.2-1, if dated, permit us to estimate the rate at which new species have formed over time. For example, the following tree indicates the timing of events in the history of the living species of Dubautia, the Hawaiian silverswords (Baldwin and Sanderson 1998), a famously diverse group of plants found only on the Hawaiian Islands.

Figure 20.2-1

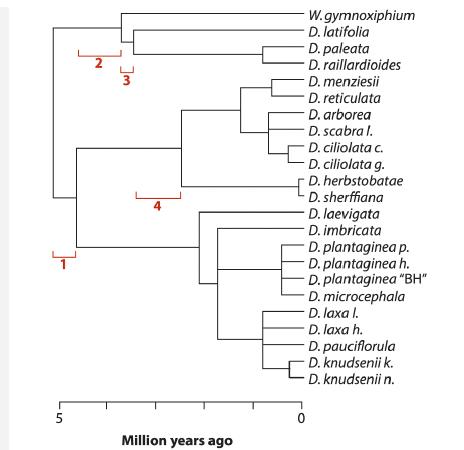
Assume that the number of Dubautia species has increased exponentially over time and has suffered no extinctions. In this case, the time interval between successive branching events on the tree provides information about the rate of increase of the number of species, λ (lambda). The earliest four intervals are indicated in red on the tree; with 23 species, there are n=21 such intervals in total. Let Y_i measure the duration of each interval i multiplied by the number of species alive at that time. We’ll call these Yi the “waiting times.” The n=21 values of Y_i from the above tree are

Under the assumptions given, the Y_i values should follow an exponential distribution (Hey 1992), with probability highest at zero and declining smoothly with increasing Y. To illustrate, an exponential distribution is superimposed on the following histogram of the Y_i values.

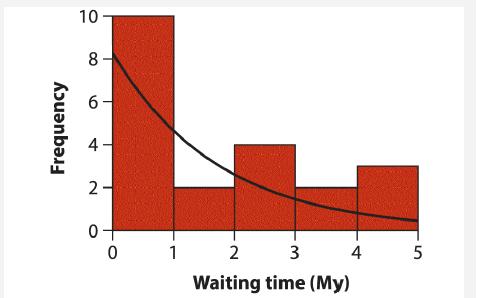
Use the waiting-time data to estimate the rate λ. The formula for the log-likelihood of λ, given the Y_i, is ln L [λ | observed waiting times] =n ln [ λ ]−λΣ_iY_i.

a. Using a computer program, calculate the log-likelihood of values of λ between 0.1 and 0.9 in increments of 0.01. Draw the relationship between the log-likelihood and λ with a log-likelihood curve.

b. Find the maximum likelihood estimate of λ to two decimal places. This estimates the number of new species produced per species per million years in Dubautia.

c. Using a similar approach as in part (b), find the likelihood-based 95% confidence interval for λ.