The Lippmann-Schwinger formalism can also be applied to a one- dimensional transmission-reflection problem with a finite-range potential, V(x) ? 0 for 0

a. Suppose we have an incident wave coming from the left: = e^1kx / ?2?. I-low must we handle the singular 1 / (E ? II₀) operator if we are to have a transmitted wave only for x > a and a reflected wave and the original wave for x (+) >.

b. Consider the special case of an attractive ?-function potential

Solve the integral equation to obtain the transmission and reflection amplitudes. Check your results with Gottfried 1966. 52.

c. The one-dimensional 8-function potential with y > 0 admits one (and only one) bound state for any value of ?. Show that the transmission and reflection amplitudes you computed have bound-state poles at the expected positions when k is regarded as a complex variable.

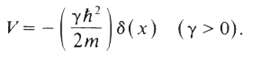
yh? 8(x) (y>0). 2m