We remarked in Impact 19.2 that the particle in a sphere is a reasonable starting point for the discussion of the electronic properties of spherical metal Nan particles. Here, we justify eqn 9.54, which shows that the energy of an electron in a sphere is quantized.

(a) The Hamiltonian for a particle free to move inside a sphere of radius R is

H = - h / 2m ∆2 Show that the Schrödinger equation is separable into radial and angular components. That is, begin by writing Ψ(r, θ, Φ) = X(r) Y (θ, Φ), where X(r) depends only on the distance of the particle away from the centre of the sphere, and Y (θ, Φ) is a spherical harmonic. Then show that the Schrödinger equation can be separated into two equations, one for X, the radial equation, and the other for Y, the angular equation:

clip_image001.emz" o:title="" blacklevel="3932f" grayscale="t"/>

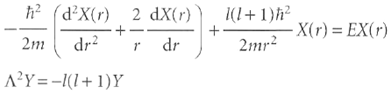
You may wish to consult further information 10.1 for additional help.

(b) Consider the case 1= 0. Show by differentiation that the solution of the radial equation has the form

X (r) = (2πR) -1/2 sin (nπr/R)/r

(c) Now go on to show that the allowed energies are given by:

E_n = n²h² / 8mR²

This result for the energy (which is eqn 9.54 after substituting m, for m) also applies when l ≠ O.

(d'x(r) 2 dX(r) ) 2mdrr dr i(1+1) 2mr x( r) = EX(r) A?Y=-1(1+1)Y