You are performing an experiment in which the concentration, CA, of a reactive species is measured as a function of time, t, at several temperatures, T. At a fixed temperature, CA varies with t according to the relation 1/C_A = 1/C_A0 + kt where CA (mol/liter) is the concentration of A at time t (min, C_A0 (mol/liter) is the initial concentration of A, and k [L/(mol ? min)] is the reaction rate constant. The rate constant in turn depends on temperature, according to the formula k = k₀ exp [? E / (8.314T)] where k₀ is constant, T (K) is the reactor temperature, and E (J/mol) is the reaction activation energy. Write a computer program that will carry out the following tasks:

(a) Read in MA, the molecular weight of A, and NT, the number of temperatures at which measurements was made.?

(b) For the first temperature, read in the value of T in ?C, the number of data points, N; and the concentrations and times (t₁, C_A1), (t₂, C_A2), . . . ,(t_n, C_An), where the times are in minutes and the concentrations are in grams of A/liter.

(c) Convert the temperature to Kelvin and the concentrations to mol A/L.

(d) Use the method of least squares (Appendix A.1) in conjunction with Equation 1 to find the value of k that best fits the data. Store the values of k and T in arrays.

(e) Print out in a neat formats the values of T (K), the converted concentrations (mol/L) and times, and k.

(f) Repeat steps (b) through (d) for the other temperatures. It will be convenient to perform the least-squares slope calculation in a subroutine, since it must be done repeatedly. Test your program on the following data: M_A = 65.0 g/mol

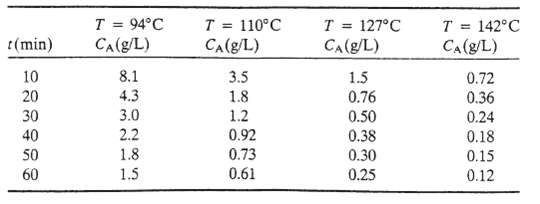
r(min) 10 20 30 40 50 60 T = 94C CA(g/L) 8.1 4.3 3.0 2.2 1.8 1.5 T = 110C CA (g/L) 3.5 1.8 1.2 0.92 0.73 0.61 T = 127C CA(g/L) 1.5 0.76 0.50 0.38 0.30 0.25 T = 142C CA (g/L) 0.72 0.36 0.24 0.18 0.15 0.12