In this problem, you will derive the expression for the average power delivered by a driving force to a driven oscillator (Figure).

(a) Show that the instantaneous power input of the driving force is given by

P = Fv AώF₀ cos wt sin (ώt – 1).

(b) Use the trigonometric identity sin (θ₁ – θ₁) = sin θ₁ cos θ₂ – cos θ₁ sin θ₂ to show that the equation in (a) can be written P = AώF₀ sin δ cos² ώt – AώF₀ cos d cos wt sin ώt.

(c) Show that the average value of the second term in your result for (b) over one or more periods is zero and that therefore.

(d) From Equation 14-50 for tan δ, construct a right triangle in which the side opposite the angle d is bώ and the side adjacent is m(ώ²₀ – ώ²), and use this triangle to show that

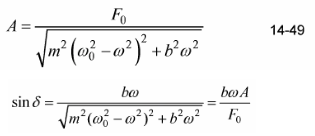
(e) Use your result for (d) to eliminate ώA so that the average power input can be written

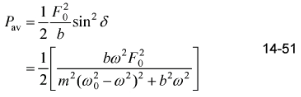
=- AoF, sin 8 Py av av