Recalculate the problem in P19.5 using a \(\Delta T_{\min }=10{ }^{\circ} \mathrm{C}\). Comment on the effect of reducing the minimum temperature difference.

[

(a) \(T_{\mathrm{C}_{\text {pinch }}}=110{ }^{\circ} \mathrm{C} ; T_{\mathrm{H}_{\text {pinch }}}=120{ }^{\circ} \mathrm{C}\);

(b) \(Q_{\mathrm{C}}=560 \mathrm{~kW} ; Q_{\mathrm{H}}=480 \mathrm{~kW}\);

(c)

\(\left.Q_{\mathrm{C}_{\text {min }}}=120 \mathrm{~kW} ; Q_{\mathrm{H}_{\text {min }}}=40 \mathrm{~kW}\right]\)

P19.5

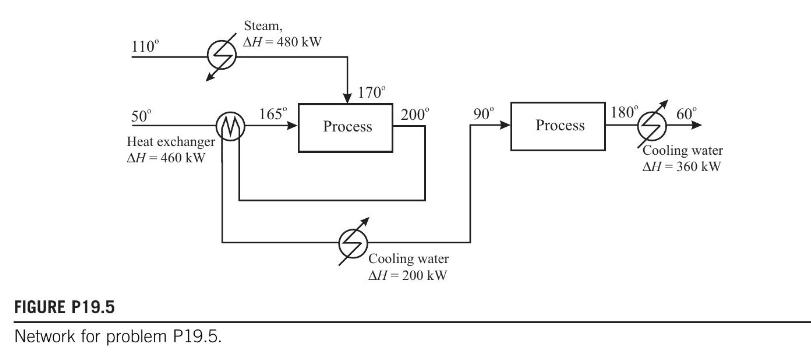
Figure P19.5 shows an existing design of a process plant, containing two exothermic processes. These require streams of reactants as shown in the diagram, and produce products at the temperatures shown. The plant achieves the necessary conditions by providing \(480 \mathrm{~kW}\) of heat from a steam source, and rejects a total of \(560 \mathrm{~kW}\) of energy to cold water utilities; only \(460 \mathrm{~kW}\) is transferred between the streams. Show

(a) that there is a pinch point, and evaluate the temperature;

(b) that the existing plant is inefficient in its use of the energy available;

(c) calculate the energy targets for \(\Delta T_{\min }=20^{\circ} \mathrm{C}\) and show a design that achieves these targets.

[

(a) \(T_{\mathrm{C}_{\text {pinch }}}=110{ }^{\circ} \mathrm{C} ; T_{\mathrm{H}_{\text {pinch }}}=130{ }^{\circ} \mathrm{C}\);

(b) \(Q_{\mathrm{C}}=560 \mathrm{~kW} ; Q_{\mathrm{H}}=480 \mathrm{~kW}\); (c)

\(\left.Q_{\mathrm{C}_{\text {min }}}=210 \mathrm{~kW} ; Q_{\mathrm{H}_{\text {min }}}=130 \mathrm{~kW}\right]\)

Transcribed Image Text:

110 Steam, AH=480 kW 50 Heat exchanger AH = 460 kW FIGURE P19.5 Network for problem P19.5. 170 165 200 90 180 60 Process Process Cooling water AH = 200 kW Cooling water AH = 360 kW