\(\Delta\) denotes the Laplace operator defined by

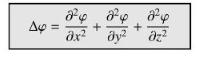
A function \(\varphi\) satisfying \(\Delta \varphi=0\) is called harmonic.
(a) Show that \(\Delta \varphi=\operatorname{div}(abla \varphi)\) for any function \(\varphi\).
(b) Show that \(\varphi\) is harmonic if and only if \(\operatorname{div}(abla \varphi)=0\).
(c) Show that if \(\mathbf{F}\) is the gradient of a harmonic function, then \(\operatorname{curl}(F)=0\) and \(\operatorname{div}(F)=0\).
(d) Show that \(\mathbf{F}(x, y, z)=\left\langle x z,-y z, \frac{1}{2}\left(x^{2}-y^{2}ight)ightangle\) is the gradient of a harmonic function. What is the flux of \(\mathbf{F}\) through a closed surface?

Ay = 24 2 + x y + 84 z