Question: (Delta) denotes the Laplace operator defined by Prove the identity [ operatorname{curl}(operatorname{curl}(mathbf{F}))=abla(operatorname{div}(mathbf{F}))-Delta mathbf{F} ] where (Delta mathbf{F}) denotes (leftlangleDelta F_{1}, Delta F_{2}, Delta F_{3}ightangle). 0x2

$\Delta$ denotes the Laplace operator defined by

0x2 ' ' +

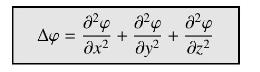
Prove the identity
\[
\operatorname{curl}(\operatorname{curl}(\mathbf{F}))=abla(\operatorname{div}(\mathbf{F}))-\Delta \mathbf{F}
\]
where $\Delta \mathbf{F}$ denotes $\left\langle\Delta F_{1}, \Delta F_{2}, \Delta F_{3}ightangle$.

0x2 ' ' +

Step by Step Solution

★★★★★

3.42 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The identity you provided is a wellknown vector calculus identity involving the curl of the curl of a vector field mathbfF This identity is given by a... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Big10Sweaters.com is a new company started last year by two recent college graduates. The idea behind the company was simple. They will sell premium logo sweaters for Big Ten colleges with one major,...

$\Delta$ denotes the Laplace operator defined by Let $\mathbf{F}=r^{n} \mathbf{e}_{r}$, where $n$ is any number, $r=\left(x^{2}+y^{2}+z^{2}ight)^{1 / 2}$, and \(\mathbf{e}_{r}=r^{-1}\langle...

$\Delta$ denotes the Laplace operator defined by A function $\varphi$ satisfying $\Delta \varphi=0$ is called harmonic. (a) Show that $\Delta \varphi=\operatorname{div}(abla \varphi)$ for any...

$\Delta$ denotes the Laplace operator defined by Prove the identity = + dx2 +

1 5 pts p ( x , t ) 5 pts q ( x , t ) ( volumetric rate ) solutions to predict the volumetric flow rate inside the system. ( c ) ( 3 0 pts ) You may consider time values at t = 1 0 ^ ( - 2 ) , 1 0 ^...

c Bosonic creation and destruction operators The creation operator at (f) is defined by at (8)|41,42, ..., N) = 14,41,42, ..., 9N) and at (0)|0)) = 18) where (0) denotes the vacuum state and (f) an...

Let $\mathcal{D}$ be the region bounded by a simple closed curve $C$. A function $\varphi(x, y)$ on $\mathcal{D}$ (whose second-order partial derivatives exist and are continuous) is called...

The Laplace operator $\Delta$ is defined by \[ \Delta \varphi=\frac{\partial^{2} \varphi}{\partial x^{2}}+\frac{\partial^{2} \varphi}{\partial y^{2}} \] For any vector field...

Find an antidifference for the sequence $\left(H_{k} ight) $ defined by $$ H_{k}=\sum_{j=1}^{k} \frac{1}{j} $$ For inspiration, you can think about the integration by parts calculation that an...

Problem 3 . ( Please don't use AI , I can tell and it doesnt give the right answer ) Given a bounded region D in R 3 , we can consider the vector space L 2 ( D ) = { F : D C | D | F | 2 d V } with...

The Laplace operator $\Delta$ is defined by \[ \Delta \varphi=\frac{\partial^{2} \varphi}{\partial x^{2}}+\frac{\partial^{2} \varphi}{\partial y^{2}} \] For any vector field...

The company is considering a purchase of equipment that would reduce its direct labor costs by $110,000 and would change its manufacturing overhead costs to 30% variable and 70% fixed (assume total...

Albany Enterprises budget included the following estimated costs for the 2015 accounting period. Depreciation on manufacturing equipment ...... $15,200 Cost of manufacturing supplies ..............

The audit committee should understand management's processes for ( select all that apply ) : Multiple select question. accumulating guidance information developing assumptions and estimates evaluate...

OVERHEAD VARIANCES Extrim Company produces monitors. Extrims plant in San Antonio uses a standard costing system. The standard costing system relies on direct labor hours to assign overhead costs to...

Why is the disk method a special case of the general slicing method?

The region R bounded by the graph of y = f(x) 0 and the x-axis on [a, b] is revolved about the line y = -2 to form a solid of revolution whose cross sections are washers. What are the inner and...

Use the general slicing method to find the volume of the following solids. The solid whose base is the region bounded by the curves y = x 2 and y = 2 - x 2 , and whose cross sections through the...

? ? ? ? ? ? ? ? ? ? ? i s a n e a s y - t o - r e a d , o f t e n s i n g l e - p a g e , r e a l - t i m e u s e r i n t e r f a c e , s h o w i n g a g r a p h i c a l p r e s e n t a t i o n o f t...

The following ciphers are monoalphabetic substitution cipher. Write a python program that decrypts the following encrypted quotations and displays the keys. 1.ejitp spawa qleji taiul rtwll rflrl...

Use a separate page for each question. You MUST show ALL calculations required to receive full credit. The calculations MUST be placed on the answer pages. Points will be subtracted for failure to...