\(\Delta\) denotes the Laplace operator defined by

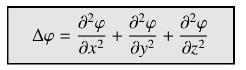
Let \(\mathbf{F}=r^{n} \mathbf{e}_{r}\), where \(n\) is any number, \(r=\left(x^{2}+y^{2}+z^{2}ight)^{1 / 2}\), and \(\mathbf{e}_{r}=r^{-1}\langle x, y, zangle\) is the unit radial vector.
(a) Calculate \(\operatorname{div}(\mathbf{F})\).
(b) Calculate the flux of \(\mathbf{F}\) through the surface of a sphere of radius \(R\) centered at the origin. For which values of \(n\) is this flux independent of \(R\) ?
(c) Prove that \(abla\left(r^{n}ight)=n r^{n-1} \mathbf{e}_{r}\).
(d) Use (c) to show that \(\mathbf{F}\) is conservative for \(n eq-1\). Then show that \(\mathbf{F}=r^{-1} \mathbf{e}_{r}\) is also conservative by computing the gradient of \(\ln r\).
(e) What is the value of \(\int_{C} \mathbf{F} \cdot d \mathbf{s}\), where \(C\) is a closed curve that does not pass through the origin?
(f) Find the values of \(n\) for which the function \(\varphi=r^{n}\) is harmonic.

+ +