If the rectangular integrator [see below (8-38)] is used in the PID transfer function in (8-52), the resulting controller is described by
\[
\frac{M(z)}{E(z)}=D(z)=K_{p}+K_{I}\left[\frac{T z}{z-1}ight]+K_{D}\left[\frac{z-1}{T z}ight]
\]
This transfer function is implemented in many commercial digital controllers. Write a difference equation required to realize this controller.

Equation 8-52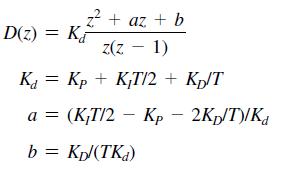

z + az + b Z(z - 1) K = Kp + KT/2 + Kp/T a = (K,T/2Kp2Kp/T)/Kd b = Kpl(TKd) D(z)= K