Suppose that a plant is described by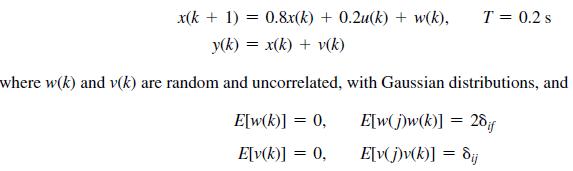

(a) Design a Kalman filter for this system. Continue the gain calculations until the gain is approximately constant. Use M(0) = 2.

(b) In part (a), we specified M(0) = 2. What are we stating about our estimate of the state x(0) ?

(c) Write the difference equations for the steady-state Kalman filter, as in part (a).

(d) Suppose that an LQ design is performed for this plant, with the resulting gain K = 0.2197. Find the control-estimator transfer function (see Fig. 9-8) for this IH-LQG design.

(e) Find the closed-loop system characteristic equation for part (d).

(f) Find the closed-loop system time constants.

(g) Suppose that the state x(k) is estimated to be 90.1 by the Kalman filter at a certain time kT. Give the three-sigma range about the value 90.1 that will almost certainly contain the true value of x(k) at that time kT.

(h) Find the system phase and gain margins.

x(k+ 1) = 0.8x(k) + 0.2u(k)+ w(k), y(k)= x(k)+v(k) where w(k) and v(k) are random and uncorrelated, with Gaussian distributions, and E[w(k)] = 0, E[v(k)] = 0, T = 0.2 s E[w(j)w(k)] = 28 if E[v(j)v(k)] = 8jj