Question: An LM test for first-order serial correlation in a fixed effects model. For (H_{5}^{b} ; ho=) 0 (given the (mu_{i}) are fixed), (a) Verify that
An LM test for first-order serial correlation in a fixed effects model. For \(H_{5}^{b} ; ho=\) 0 (given the \(\mu_{i}\) are fixed),
(a) Verify that the likelihood is given by (5.40) and derive the MLE of the \(\mu_{i}\).
(b) Using (5.34) and (5.35), verify that the LM statistic for \(H_{5}^{b}\) is given by (5.42).
(c) Verify that for \(H_{5}^{a} ; \lambda=0\) (given the \(\mu_{i}\) are fixed), one obtains the same LM statistic as in (5.42).
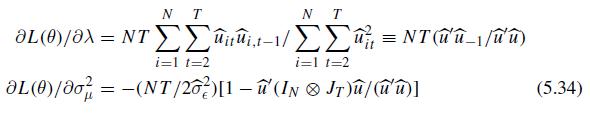
![= (NT /26?)[1 - (IN & Jr)/(t)] (5.34)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1709/2/7/2/28665e16cde2b3ae1709272284806.jpg)
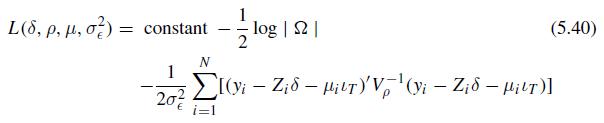
![]()
NT 1-1 =NT(_1/un) i=1 t=2 NT 8L(0)/0 = NT i=1 t=2 L(0)/06 = (NT /26?)[1 - (IN & Jr)/(t)] (5.34)
Step by Step Solution
3.50 Rating (153 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


