Each morning between 6:30 Am and 8:00Am Bill leaves the Melbourne suburb of Carnegie to drive to work at the University of Melbourne. The time it takes Bill to drive to work (TIME), depends on the departure time (DEPART), the number of red lights that he encounters (REDS), and the number of trains that he has to wait for at the Murrumbeena level crossing (TRAINS). Observations on these variables for the 249 working days in 2015 appear in the data file commute5. TIME is measured in minutes. DEPART is the number of minutes after 6:30AM that Bill departs. Consider the equation

and suppose assumptions MR1-MR5 hold.

a. Test the following joint hypotheses using a \(5 \%\) significance level:
i. The expected delay from a red light is 1.8 minutes and the expected delay from a train is 3.2 minutes.

ii. The expected delay from a red light is 2 minutes and the expected delay from a train is 3 minutes.

iii. The expected delay from a train is 3.5 minutes and the delay from a train is double that from a red light.

iv. The expected delay from a train is 3.5 minutes and the delay from a train is double that from a red light and leaving at 7:30AM instead of 7:00AM makes the trip 10 minutes longer.

b. Bill suspects that the later he leaves, the more likely he is to encounter a train. Test this hypothesis at a \(5 \%\) significance level using estimates from the model

Is there any evidence of a relationship between the number of trains and the number of red lights?

c. Show that

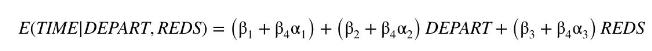
d. Regress TIME on DEPART and REDS to get estimates for \(\delta_{1}=\beta_{1}+\beta_{4} \alpha_{1}, \delta_{2}=\beta_{2}+\beta_{4} \alpha_{2}\), and \(\delta_{3}=\beta_{3}+\beta_{4} \alpha_{3}\). Using these estimates and those from (a) and (c), show that \(\hat{\delta}_{1}=b_{1}+b_{4} \hat{\alpha}_{1}\), \(\hat{\delta}_{2}=\left(b_{2}+b_{4} \hat{\alpha}_{2}\right)\), and \(\hat{\delta}_{3}=b_{3}+b_{4} \hat{\alpha}_{3}\), where \(b_{k}\) denotes an OLS estimate from the original equation.

e. Interpret \(b_{2}\) and \(\hat{\delta}_{2}\). Why are they different? How would you characterize any omitted variable bias?

Transcribed Image Text:

TIME = B + BDEPART+ 3REDS + BTRAINS + e