Question: Show that the bound given in Equation 7.6 is maximised (i.e. equal to the true (log) marginal likelihood) when (Q(boldsymbol{theta})) is identical to the true

Show that the bound given in Equation 7.6 is maximised (i.e. equal to the true $\log$ marginal likelihood) when $Q(\boldsymbol{\theta})$ is identical to the true posterior $p(\boldsymbol{\theta} \mid \mathbf{X})$.

Data from Equation 7.6

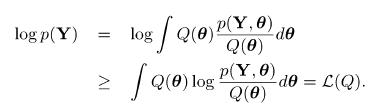
log p(Y) = IV log/Q(6) P(Y, 0) Q(0) p(Y, 0) Q(0) log

log p(Y) = IV log/Q(6) P(Y, 0) Q(0) p(Y, 0) Q(0) log Q(0) -de de = L(Q).

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Machine Learning Questions!

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

answer all questions as instructed below. attend all questions. 4 Computer Vision (a) Explain why such a tiny number of 2D Gabor wavelets as shown in this sequence are so efficient at representing...

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

3.30 VC-dimension generalization bound { realizable case. In this exercise we show that the bound given in corollary 3.19 can be improved to O( d log(m=d) m ) in the realizable setting. Assume we are...

Let N be an NFA with k states that recognizes some language A. a. Show that if A is nonempty, A contains some string of length at most k. b. Show, by giving an example, that part (a) is not...

1 . 6 4 Let N be an NFA with k states that recognizes some language A . a . Show that if A is nonempty, A contains some string of length at most k . b . Show, by giving an example, that part ( a ) is...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Consider the following decision problem on graphs, called Bound Problem. We are given an undi- rected graph G with n vertices and a list, called L, of n non-negative integers, as well a bound b. The...

One goal of the Dodd-Frank Wall Street reform is to end the too big to fail problem. How does it propose to do so? Why might it fail?

I signed a contract to purchase 20,000 units of t-shirts from a Turkish company in July of 2017 at the price of 0.5 Turkish lira per piece. The delivery and full payment is to be made in May 2018. In...

What are correlation matrices, and why do you have them?

DE4-4 Consider the Income Statement columns and the Balance Sheet columns of the work sheet in Exhibit 4-6, on the acetates between pages 130 and 131 1. What balance does the Owner's Capital account...

Ratner and Miller (2001) wondered whether people are uncomfortable when they act in a way thats not obviously in their own self-interest. They randomly assigned 33 women and 32 men to read a...

Eleanor Barkhorn (2012) reported in the Atlantic about differences in womens and mens negotiating styles. She first explained that researchers did not find a significant difference in how likely...

Hugenberg, Miller, and Claypool (2007) conducted a study to better understand the cross-race effect, in which people have a difficult time recognizing members of different racial groupscolloquially...

Required information Use the following information for the Exercises 12-13 below. (Algo) [The following information applies to the questions displayed below.] Del Gato Clinic's cash account shows an...

On October 1 , 2 0 2 0 , Bramble Company establishes an imprest petty cash fund by issuing a check for $ 1 8 0 to Pat Harmon, the custodian of the petty cash fund. On October 3 1 , 2 0 2 0 , Pat...

The following list of balances was extracted from the books of Unicomer Ltd, on December 31. 2017. The following notes are relevant: i. Inventory at 31 December 2017 was valued at $800000. ii....