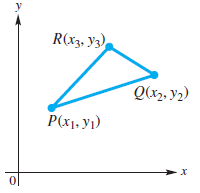
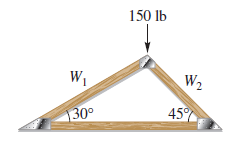
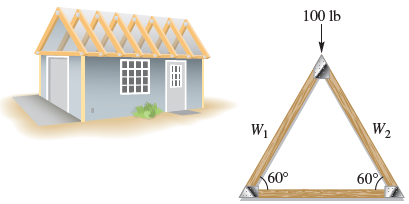
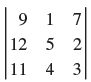
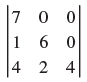
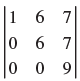
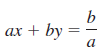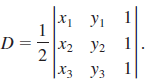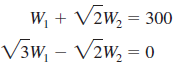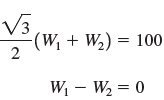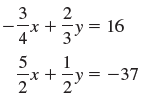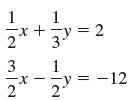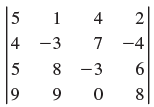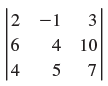New Semester
Started
Get
50% OFF
Study Help!
--h --m --s
Claim Now
Question Answers
Textbooks
Find textbooks, questions and answers
Oops, something went wrong!
Change your search query and then try again
S
Books
FREE
Study Help
Expert Questions
Accounting
General Management
Mathematics
Finance
Organizational Behaviour
Law
Physics
Operating System
Management Leadership
Sociology
Programming
Marketing
Database
Computer Network
Economics
Textbooks Solutions
Accounting
Managerial Accounting
Management Leadership
Cost Accounting
Statistics
Business Law
Corporate Finance
Finance
Economics
Auditing
Tutors
Online Tutors
Find a Tutor
Hire a Tutor
Become a Tutor
AI Tutor
AI Study Planner
NEW
Sell Books
Search
Search
Sign In
Register
study help
mathematics
college algebra
College Algebra 12th edition Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels - Solutions
Solve each system, using the method indicated, if possible.(Cramer’s rule)7x + y - z = 42x - 3y + z = 2-6x + 9y - 3z = -6
Solve each system, using the method indicated, if possible.(Gauss-Jordan)2x + 4y + 4z = 4x + 3y + z = 4-x + 3y + 2z = -1
Solve each system, using the method indicated, if possible.(Elimination)x + y + z = 1-x + y + z = 5y + 2z = 5
Solve each system, using the method indicated, if possible.(Cramer’s rule)5x + 2y = -34x - 3y = -30
Solve each system, using the method indicated, if possible.(Gauss-Jordan)3x + 5y = -5-2x + 3y = 16
Solve each system, using the method indicated, if possible.(Elimination)2x - 3y = 185x + 2y = 7
Solve each system, using the method indicated, if possible.(Elimination)x - y = 6x - y = 4
Solve each system, using the method indicated, if possible.(Substitution)5x + 10y = 10x + 2y = 2
Solve each system, using the method indicated, if possible.(Substitution)2x + y = -4-x + 2y = 2
Find the partial fraction decomposition for the rational expression. 2x + 4 x3 – 2x2
Find the partial fraction decomposition for the rational expression. 4x2 - — Зх — 4 х3 + x2 — 2х
Find the partial fraction decomposition for the rational expression. — 2х2 — 24 х4 — 16
Find the partial fraction decomposition for the rational expression. .2 х4 — 1
Find the partial fraction decomposition for the rational expression. 3x6 + 3x4 + 3x x4 + x2
Find the partial fraction decomposition for the rational expression. 5x + 10x4 – 15x3 + 4x2 + 13x – 9 x3 + 2x2 – 3x
Find the partial fraction decomposition for the rational expression. 3x* + x3 + 5x² – x + 4 (x – 1)(x² + 1)²
Find the partial fraction decomposition for the rational expression. -x4 — 8х2 + Зх — 10 (x + 2)(x² + 4)²
Find the partial fraction decomposition for the rational expression. x4 + 1 x(x² + 1)2
Find the partial fraction decomposition for the rational expression. Зх — 1 x(2x² + 1)²
Find the partial fraction decomposition for the rational expression. 6x5 + 7x4 — х? + 2x Зx2 + 2х 1
Find the partial fraction decomposition for the rational expression. 2x5 + 3x* – 3x³ – 2x2 + x 2x2 + 5x + 2
Find the partial fraction decomposition for the rational expression. 3 x(х + 1)(х? + 1)
Find the partial fraction decomposition for the rational expression. x(2x + 1)(3x² + 4)
Find the partial fraction decomposition for the rational expression. 2x + 1 (x + 1)(x² + 2)
Find the partial fraction decomposition for the rational expression. Зх — 2 (x + 4)(3x² + 1)
Find the partial fraction decomposition for the rational expression. x²(x? – 2)
Find the partial fraction decomposition for the rational expression. -3 x²(x² + 5)
Find the partial fraction decomposition for the rational expression. х3 + 2 х3 — Зх2 + 2х
Find the partial fraction decomposition for the rational expression. x3 + 4 9х3 — 4х
Find the partial fraction decomposition for the rational expression. x²(x + 3)
Find the partial fraction decomposition for the rational expression. x2 x2 + 2x + 1
Find the partial fraction decomposition for the rational expression. 2x (x + 1)(x + 2)²
Find the partial fraction decomposition for the rational expression. 2х + 1 (х + 2)3
Find the partial fraction decomposition for the rational expression. 3 (x+ 1)(x+ 3)
Find the partial fraction decomposition for the rational expression. 4x? — х — 15 x(x + 1) (х — 1)
Find the partial fraction decomposition for the rational expression. x(х — 3)
Find the partial fraction decomposition for each rational expression. 4 x(1 – x)
Find the partial fraction decomposition for each rational expression. 5х — 3 х2 — 2х — 3
Find the partial fraction decomposition for each rational expression. х х2 + 4х — 5
Find the partial fraction decomposition for each rational expression. (x + 1)(x - 1)
Find the partial fraction decomposition for the rational expression. 4х + 2 (x + 2)(2x – 1)
Find the partial fraction decomposition for each rational expression. Зх — 1 x(х + 1)
Find the partial fraction decomposition for each rational expression. 3x(2x + 1)
Answer the question.In Exercise 5, after clearing fractions to decompose, the equation3x - 1 = A(2x2 + 1)2 + (Bx + C)(x)(2x2 + 1) + (Dx + E)(x)results. If we let x = 0, what is the value of A?
Answer the question.By what expression should we multiply each side ofso that there are no fractions in the equation? Dx + E (2г2 + 1)2 Зх — 1 Вх + C x(2к? + 1)? 2x2 + 1 х
In Exercise 3, after clearing fractions to decompose, the equation 3x - 2 = A(3x2 + 1) + (Bx + C)(x + 4) results. If we let x = -4, what is the value of A?Exercise 3 3x – 2 A Bx + C (x + 4)(3x2 + 1) x+4 3x2 + 1
Answer the question.By what expression should we multiply each side ofso that there are no fractions in the equation? Зх — 2 |(х+ 4)(3x2 + 1) Вх + C Зх? + 1 х+4
In Exercise 1, after clearing fractions to decompose, the equation A(2x + 1) + B(3x) = 5 results. If we let x = 0, what is the value of A?Exercise 1 A + 3x B Зx (2х + 1) 2х + 1
Answer each question.By what expression should we multiply each side ofso that there are no fractions in the equation? B A Зх 2х + 1 Зx(2х + 1)
The determinant of a 3 × 3 matrix A is defined as follows.Does the method of evaluating a determinant using “diagonals” extend to 4 × 4 matrices? a12 a13 fA 3 | а21 аzz аз |, then |А азі аз2 аз. a11 a13 a12 аз a21 a22 азз |аз1 аз2 Е (аја2азз + а12а23а31 +
Exercise 112. Evaluate the determinant by expanding about column 1 and using the method of cofactors. Do these methods give the same determinant for 3 × 3 matrices?Exercise 112Evaluate the determinantusing the method of “diagonals.” |1 3 2 2 6
The determinant of a 3 × 3 matrix A is defined as follows.Evaluate the determinantusing the method of “diagonals.” a12 a13 fA 3 | а21 аzz аз |, then |А азі аз2 аз. a11 a13 a12 аз a21 a22 азз |аз1 аз2 Е (аја2азз + а12а23а31 + aјзаz1аз2) — (азја2а13 +
The determinant of a 3 × 3 matrix A is defined as follows.The determinant of a 3 × 3 matrix can also be found using the method of “diagonals.”Step 1 Rewrite columns 1 and 2 of matrix A to the right of matrix A.Step 2 Identify the diagonals d1 through d6 and multiply their elements.Step 3 Find
In the following system, a, b, c, . . . , l are consecutive integers. Express the solution set in terms of z.ax + by + cz = dex + ƒy + gz = hix + jy + kz = l
Use Cramer’s rule to find the solution set if a, b, c, d, e, and ƒ are consecutive integers.ax + by = cdx + ey = ƒ
Solve each system for x and y using Cramer’s rule. Assume a and b are nonzero constants.x + by = bax + y = a
Solve each system for x and y using Cramer’s rule. Assume a and b are nonzero constants.b2x + a2y = b2ax + by = a
Solve each system for x and y using Cramer’s rule. Assume a and b are nonzero constants. ах + by
Solve each system for x and y using Cramer’s rule. Assume a and b are nonzero constants.bx + y = a2ax + y = b2
Write the sign array representing (-1)i+j for each element of a 4 × 4 matrix.
Find the area of a triangular lot whose vertices have the following coordinates in feet. Round the answer to the nearest tenth of a foot. (101.3, 52.7), (117.2, 253.9), and (313.1, 301.6)
A triangle with vertices at (x1, y1), (x2, y2), and (x3, y3), as shown in the figure, has area equal to the absolute value of D, whereFind the area of each triangle having vertices at P, Q, and R.P(2, -2), Q(0, 0), R(-3, -4) |x, У1 |X2 Уг |X3 Уз R(xз- Уз). Осх, У2) Р(
A triangle with vertices at (x1, y1), (x2, y2), and (x3, y3), as shown in the figure, has area equal to the absolute value of D, whereFind the area of each triangle having vertices at P, Q, and R.P(2, 5), Q(-1, 3), R(4, 0) |x, У1 |X2 Уг |X3 Уз R(xз- Уз). Осх, У2) Р(
A triangle with vertices at (x1, y1), (x2, y2), and (x3, y3), as shown in the figure, has area equal to the absolute value of D, whereFind the area of each triangle having vertices at P, Q, and R.P(0, 1), Q(2, 0), R(1, 5) |x, У1 |X2 Уг |X3 Уз R(xз- Уз). Осх, У2) Р(
A triangle with vertices at (x1, y1), (x2, y2), and (x3, y3), as shown in the figure, has area equal to the absolute value of D, whereFind the area of each triangle having vertices at P, Q, and R.P(0, 0), Q(0, 2), R(1, 4) |x, У1 |X2 Уг |X3 Уз R(xз- Уз). Осх, У2) Р(
(Refer to Exercise 87.) Use the following system of equations to determine the forces or weights W1 and W2 exerted on each rafter for the truss shown in the figure.Exercise 87.The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If
The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If a 100-pound force is applied at the peak of the truss, then the forces or weights W1 and W2 exerted parallel to each rafter of the truss are determined by the following linear
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.5x - 2y = 34y + z = 8x + 2z = 4
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.x + 2y = 103x + 4z = 7-y - z = 1
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.3x + 5y = -72x + 7z = 24y + 3z = -8
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.5x - y = -43x + 2z = 44y + 3z = 22
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.2x - 3y + z - 8 = 0-x - 5y + z + 4 = 03x - 5y + 2z - 12 = 0
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.4x - 3y + z + 1 = 05x + 7y + 2z + 2 = 03x - 5y - z - 1 = 0
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.3x - 2y + 4z = 14x + y - 5z = 2-6x + 4y - 8z = -2
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.-2x - 2y + 3z = 45x + 7y - z = 22x + 2y - 3z = -4
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.2x - y + 3z = 1-2x + y - 3z = 25x - y + z = 2
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.x + 2y + 3z = 44x + 3y + 2z = 1-x - 2y - 3z = 0
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.x + y + z = 42x - y + 3z = 44x + 2y - z = -15
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.2x - y + 4z = -23x + 2y - z = -3x + 4y + 2z = 17
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set. 3 2 3 -37 2
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set. = 2 31 3 -12 2
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.4x + 3y = 912x + 9y = 27
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.3x + 2y = 46x + 4y = 8
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.12x + 8y = 31.5x + y = 0.9
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.1.5x + 3y = 52x + 4y = 3
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.3x + 2y = -45x - y = 2
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.5x + 4y = 103x - 7y = 6
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.4x - y = 02x + 3y = 14
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.4x + 3y = -72x + 3y = -11
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.3x + 2y = -42x - y = -5
Use Cramer’s rule to solve each system of equations. If D = 0, then use another method to determine the solution set.x + y = 42x - y = 2
Use the determinant theorems to evaluate each determinant. 5 -1 -1 4 2 -3 1 -5 3 0 -2
Use the determinant theorems to evaluate each determinant. 5 -1 3 -6 2 -1 3 -6 4 -7 3 1 2.
Use the determinant theorems to evaluate each determinant. -2 0 3 6 3 2 -1
Use the determinant theorems to evaluate each determinant. 5 4 2 7 -4 4 -3 8 -3
Use the determinant theorems to evaluate each determinant. |-1 0 5 4 -3 3 8 2 9 -5 4 4 -1 10 2.
Use the determinant theorems to evaluate each determinant. 9 1 12 5 2 11 4 3
Use the determinant theorems to evaluate each determinant. 2 -1 3 4 10 4 5 6.
Use the determinant theorems to evaluate each determinant. 4 2 4
Use the determinant theorems to evaluate each determinant. |1 6 7
Showing 12300 - 12400
of 16373
First
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
Last
Step by Step Answers
Get 50% OFF
Claim Now
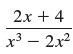
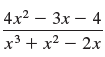
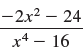
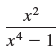
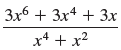
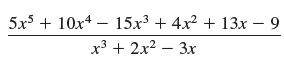
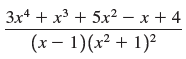
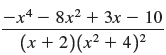
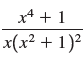
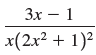
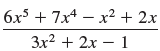
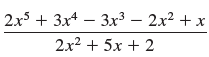
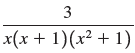
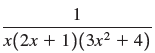
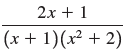
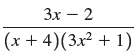
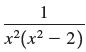
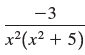
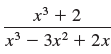
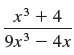
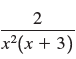
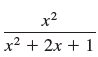
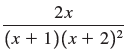
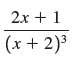
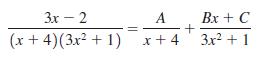
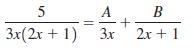
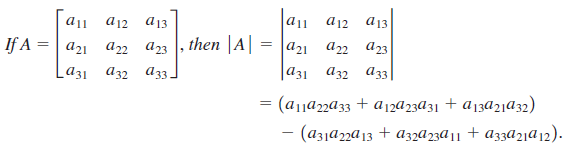
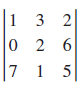
![a21 a22 Lasi a2 d. d d #33] a31 U32 'p. dz dz Each d is a product.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/9/5/2/1465c80e912a5a7f1551790530582.jpg)
