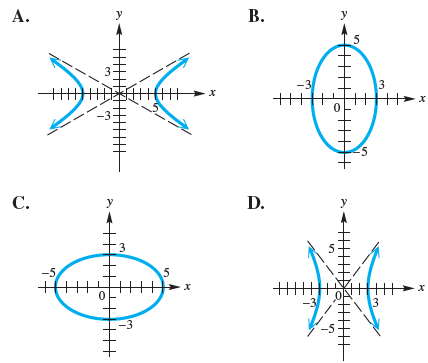
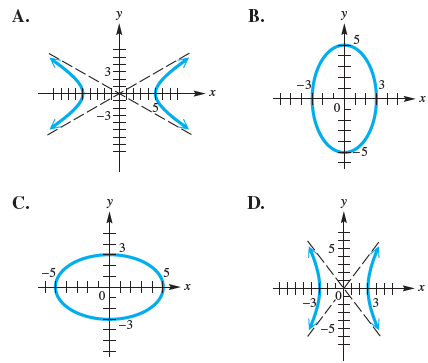
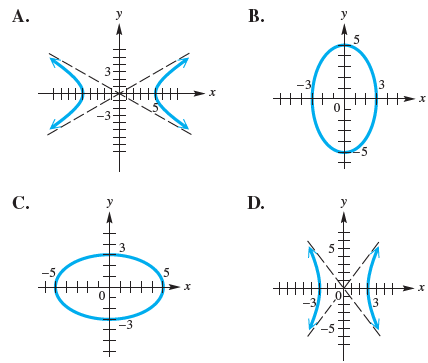
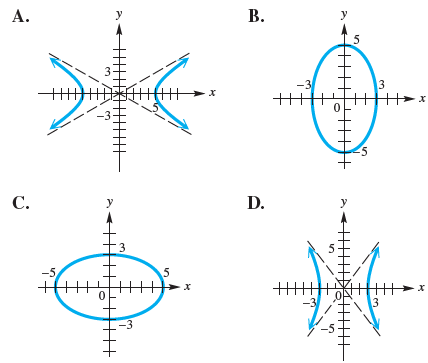
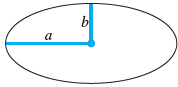
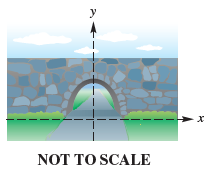
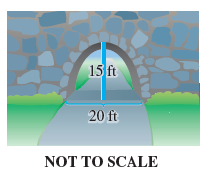
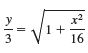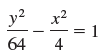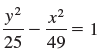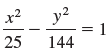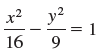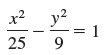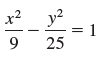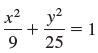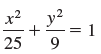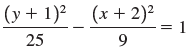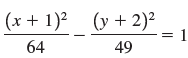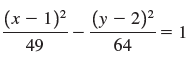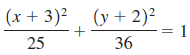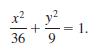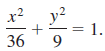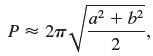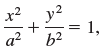![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


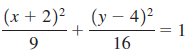
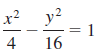
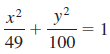
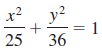
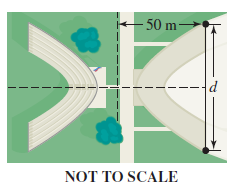

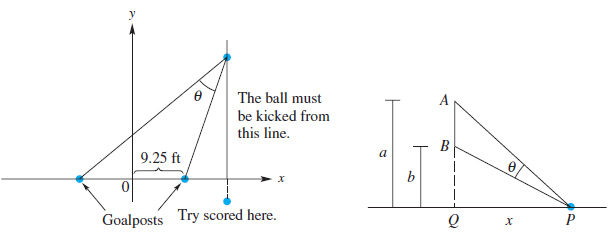
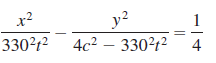
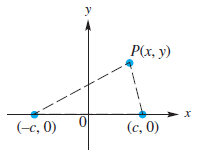
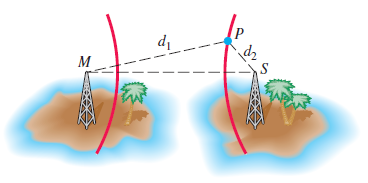

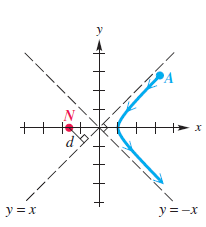
![x2 1; [-10, 10] by 49 [– 10, 10] 25 ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/4/8/3/5575c8904e5cc6b31552466311507.jpg)
![y2 = 1; [-6.6, 6.6] by [-8, 8] х 4 16 4+](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/4/8/3/4965c8904a8e1e811552466250546.jpg)