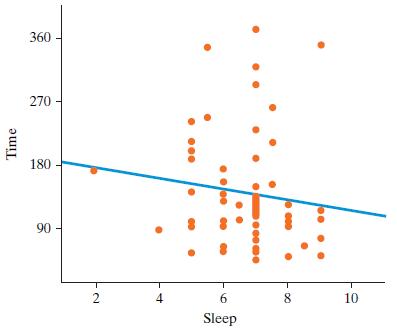
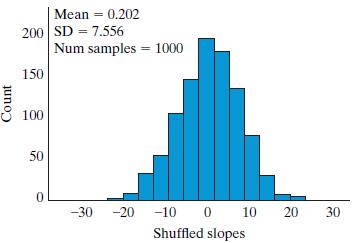
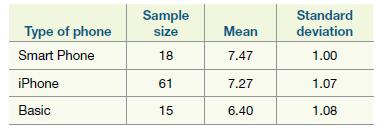
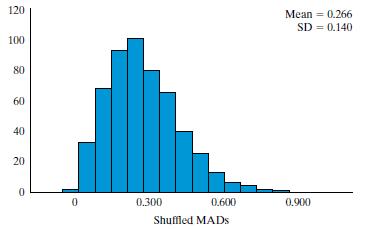
Introductory Statistics 9th Edition Prem S. Mann - Solutions

Discover the complete solutions for "Introductory Statistics 9th Edition" by Prem S. Mann, available for online access. This resource provides an extensive answers key and solutions manual, perfect for understanding complex concepts. Access solutions in PDF format and explore solved problems for every chapter. With a comprehensive test bank and chapter solutions, students can confidently tackle any question. Benefit from step-by-step answers, an instructor manual, and textbook guidance. All solutions are crafted to enhance learning and are available for free download, making it an essential tool for mastering statistics.