![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


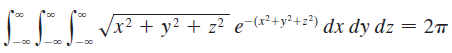
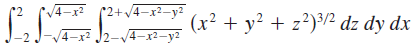
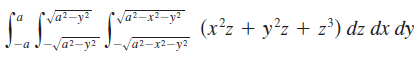
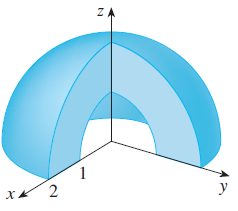
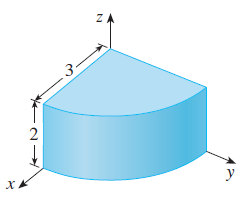
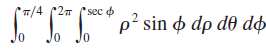
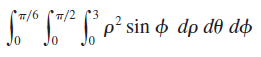

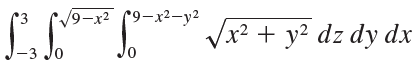
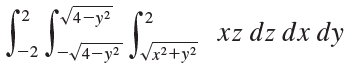
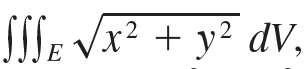
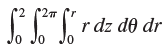
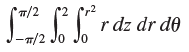
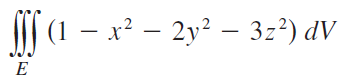
![1 fave V(E) J] F(x, y, z) dV](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/1/8/9/9805c93cc5c560761553172746426.jpg)