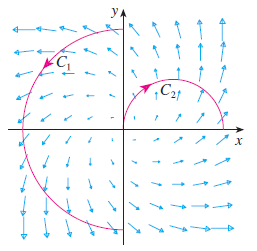
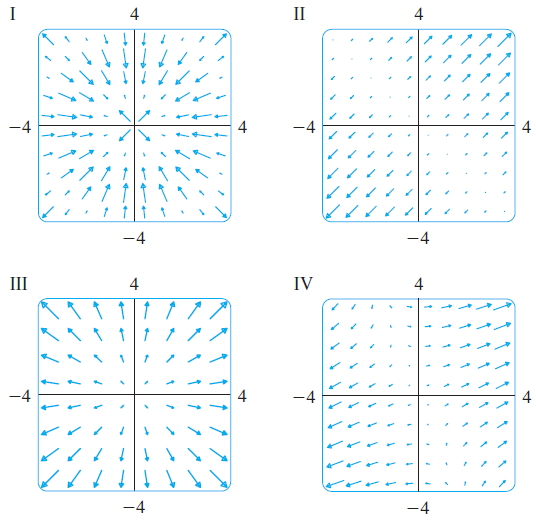
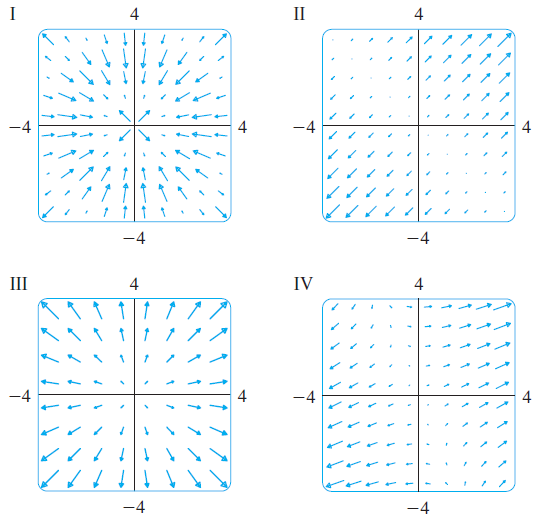
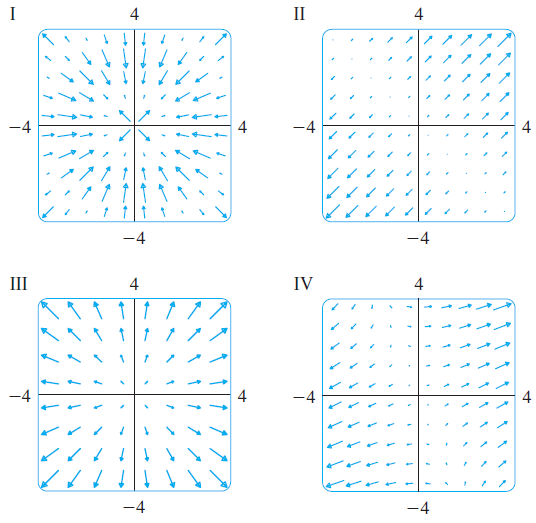
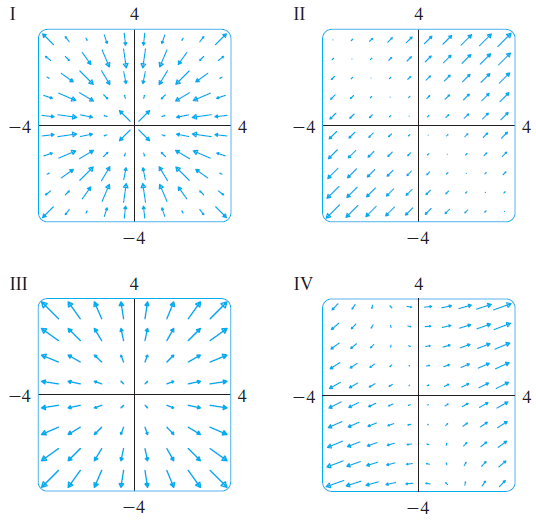
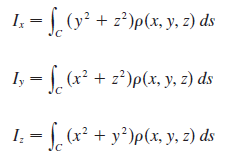![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


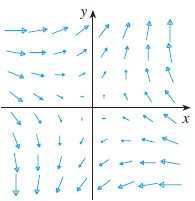
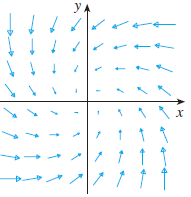
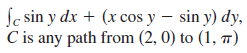
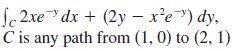
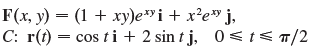
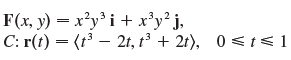
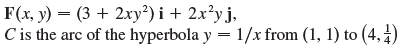
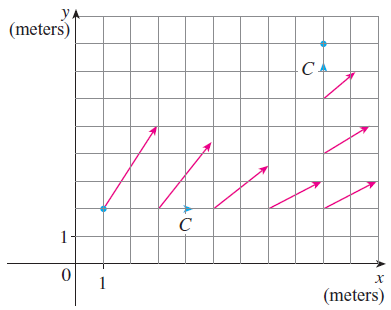
![r- dr = {[Ir(b)P° – |r(a)|]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/2/7/8/1165c9524a4b33a91553260891887.jpg)