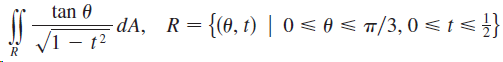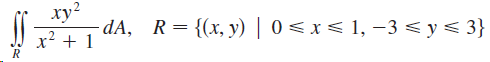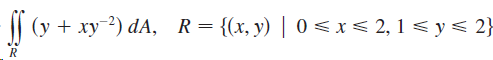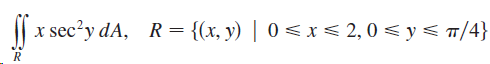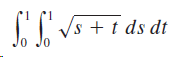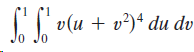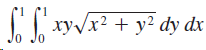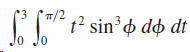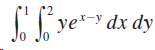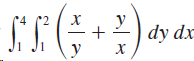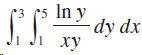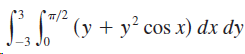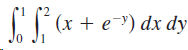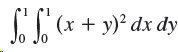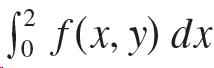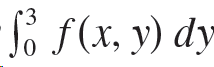![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


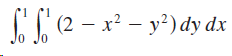
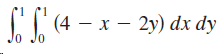
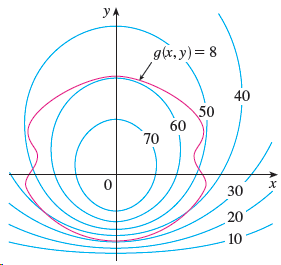
![1 R=[1,3]× [1, 2] -dA, 1 + x + y](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/1/0/7/5665c928a6ec28de1553090331504.jpg)
![yey dA, R= [0, 2] × [0, 3] —ху](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/1/0/7/5455c928a59c0d501553090310457.jpg)
![R=[0, 1] × [0, 1] -dA, 1+ ху](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/1/0/7/5295c928a49f27281553090294620.jpg)
![x sin(x + y) dA, R= [0, T/6] × [0, 1/3]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/1/0/7/5145c928a3a4f49d1553090279033.jpg)