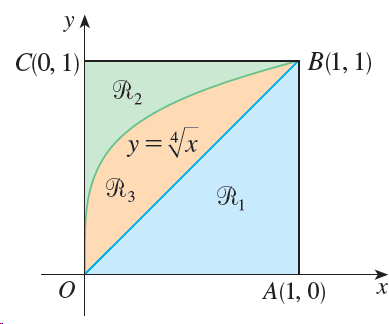
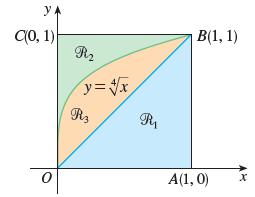
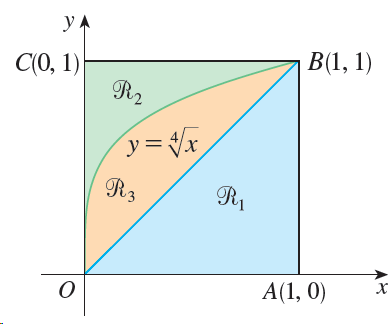
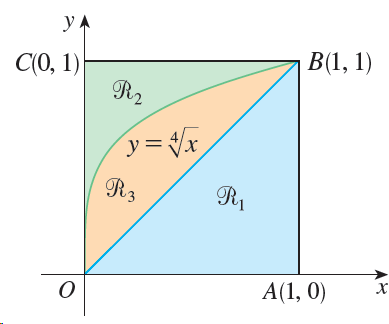
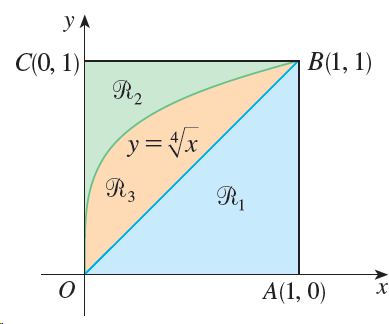
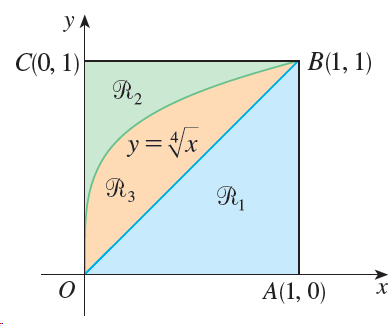
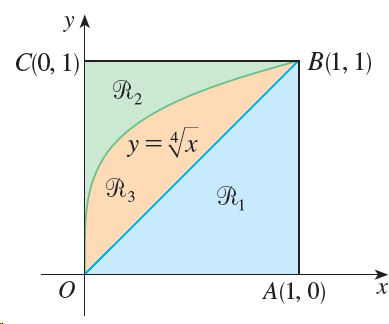
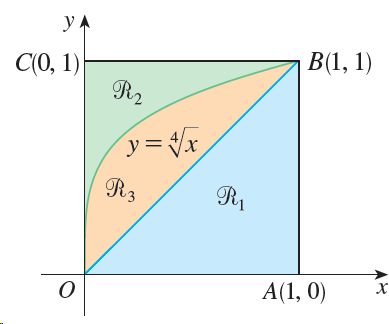
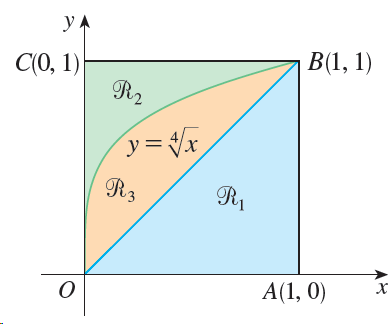
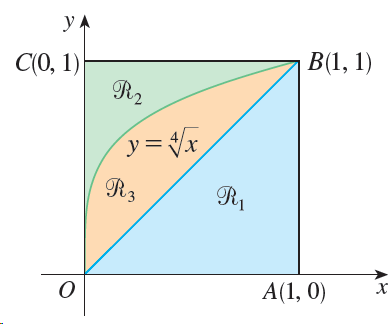
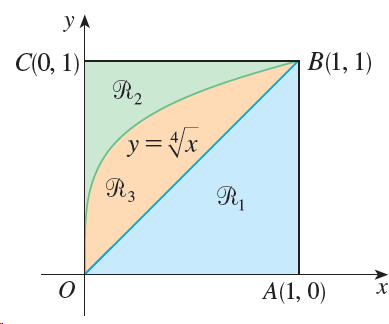
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![[0, п] h(x) = cos*x sin x,](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/0/8/0065c758e463df7a1551190723307.jpg)
![f(x) = x²/(x³ + 3)², [-1, 1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/0/7/9935c758e39eefd51551190711066.jpg)
![sin t cos t, [0, п/2] f(t) = e](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/0/7/9825c758e2e87bfc1551190699633.jpg)
![[1, 3] g(t): V3 + t?](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/0/7/9685c758e2029c371551190685245.jpg)
![f(x) = Vx, [0, 4]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/0/7/8465c758da696a131551190563679.jpg)
![— Зх? + 8х, Г-1, 2] f(x)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/2/0/7/8165c758d88c6bdb1551190533852.jpg)
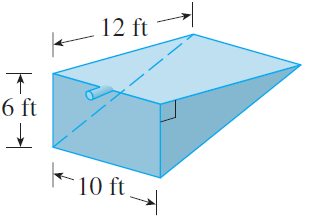
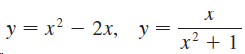
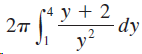
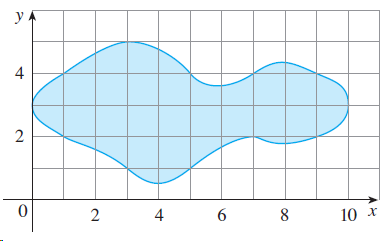
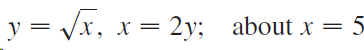
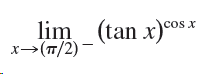
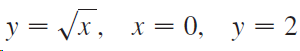
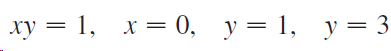
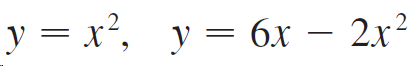
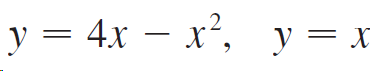
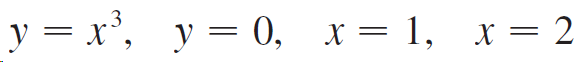
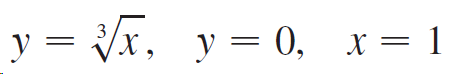
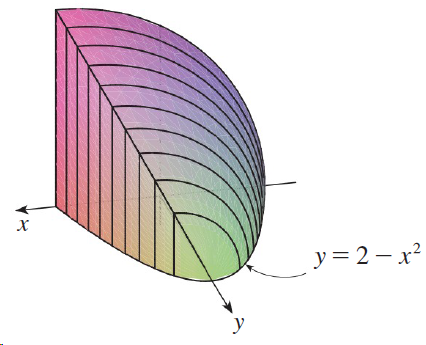
![dx -В- ]ак (3 – т](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/9/3/2/8455c715b6d2d7691550915561985.jpg)