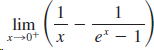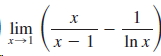![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


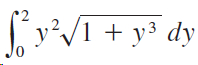
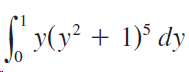
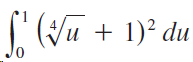
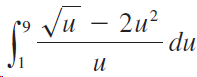
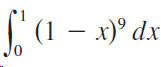
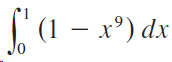
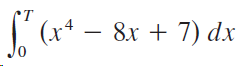
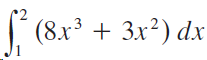
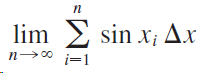
![9, SLS)g(x)] dx• g(x) dx %3| f(x) dx](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/7/4/5/1205c6e7e2030c971550727832204.jpg)
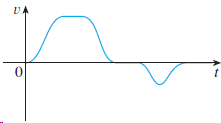
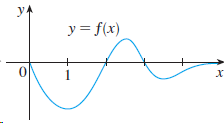
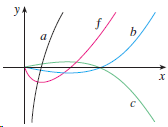
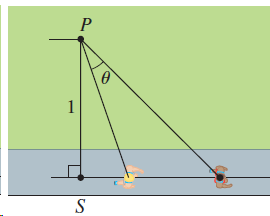
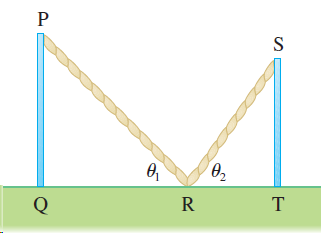
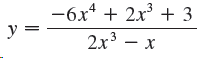
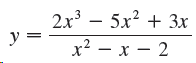
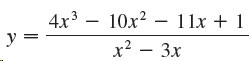
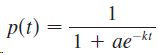
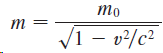
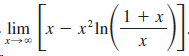
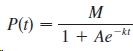
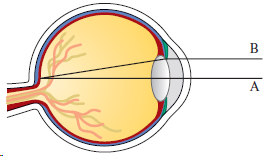
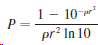
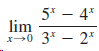
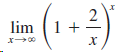
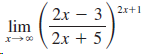
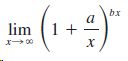
![lim [In(x' – 1) - In(x³ – 1)]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/5/9/0/5755c8aa6efa37171552616523628.jpg)