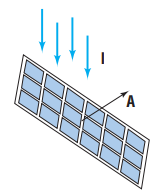
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


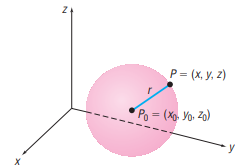
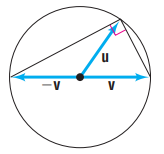
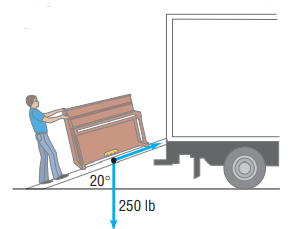
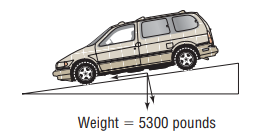
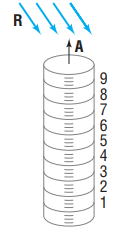
![M[(cos a)i + (cos B)j + (cos y)k] (7)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/0/0/0/3355c90e78f573e11552686764248.jpg)
![M[(cos a)i + (cos B)j + (cos y)k] (7)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/0/0/0/3295c90e789ee6b31552686758871.jpg)
![= ||M[(cos a)i + (cos B)j + (cos y)k] (7) V](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/0/0/0/3245c90e7844de781552686753200.jpg)
![M[(cos a)i + (cos B)j + (cos y)k] (7)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/0/0/0/3185c90e77e939121552686747495.jpg)
![M[(cos a)i + (cos B)j + (cos y)k] (7)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/0/0/0/3115c90e777c9bf51552686740692.jpg)
![M[(cos a)i + (cos B)j + (cos y)k] (7)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/0/0/0/3545c90e7a2ac3971552686783602.jpg)