For the system in Figure 3.57, the forcing per unit mass is \(F(t) / m=10 \sin 15 t \mathrm{ft} / \mathrm{s}^{2}\). Solve for the transient response, the steady-state response, and the constants of integration for the following initial conditions.

(a) \(x(0)=0\) in, \(\dot{x}(0)=5 \mathrm{in} / \mathrm{s}\)

(b) \(x(0)=5\) in, \(\dot{x}(0)=0 \mathrm{in} / \mathrm{s}\)

(c) \(x(0)=5\) in, \(\dot{x}(0)=5 \mathrm{in} / \mathrm{s}\).

For the parameter values \(W=40 \mathrm{lb}, c=0.85 \mathrm{lb}-\) \(\mathrm{s} /\) in, \(k=12.5 \mathrm{lb} /\) in, write down the complete response. Plot the transient and steady-state responses separately, then plot both of these with the complete solution on the same graph. Compare the results and discuss the significance of the initial conditions on the total response as time evolves.

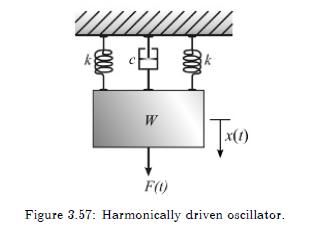
e000 6000 W F(t) Figure 3.57: Harmonically driven oscillator.