Question: Suppose we obtain a kernel density estimate using the uniform kernel (see Table 9.1) with (h=1) and a sample of size (N=100). Suppose in fact
Suppose we obtain a kernel density estimate using the uniform kernel (see Table 9.1) with \(h=1\) and a sample of size \(N=100\). Suppose in fact the data \(x \sim \mathcal{N}[0,1]\).
(a) Calculate the bias of the kernel density estimate at \(x_{0}=1\) using (9.4).
(b) Is the bias large relative to the true value \(\phi(1)\), where \(\phi(\cdot)\) is the standard normal pdf?
(c) Calculate the variance of the kernel density estimate at \(x_{0}=1\) using (9.5).
(d) Which is making a bigger contribution to MSE at \(x_{0}=1\), variance or bias squared?
(e) Using results in Section 9.3.7, give a \(95 \%\) confidence interval for the density at \(x_{0}=1\) based on the kernel density estimate \(\widehat{f}(1)\).
(f) For this example, what is the optimal bandwidth \(h^{*}\) from (9.10).
![b(xo) =E[f(xo)] = f(x0) = = h "(x) zK (z)dz. (9.4)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1715/7/6/7/6606644896cd04021715767660993.jpg)
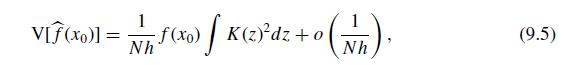
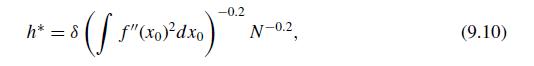


b(xo) =E[f(xo)] = f(x0) = = h "(x) zK (z)dz. (9.4)
Step by Step Solution
3.42 Rating (152 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


