Suppose we obtain a kernel regression estimate using a uniform kernel (see Table 9.1) with \(h=1\) and a sample of size \(N=100\). Suppose in fact the data \(x \sim \mathcal{N}[0,1]\) and the conditional mean function is \(m(x)=x^{2}\).

(a) Calculate the bias of the kernel regression estimate at \(x_{0}=1\) using (9.23).

(b) Is the bias large relative to the true value \(m(1)=1\) ?

(c) Calculate the variance of the kernel regression estimate at \(x_{0}=1\) using (9.24).

(d) Which is making a bigger contribution to MSE at \(x_{0}=1\), variance or bias squared?

(e) Using results in Section 9.5.4, give a \(95 \%\) confidence interval for \(\mathrm{E}\left[y \mid x_{0}=1\right]\) based on the kernel regression estimate \(\widehat{m}(1)\).

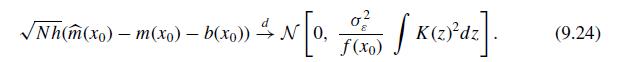
= b(xo) h (m'(xo). : (m f'(xo) + f(xo) m" (xo)) zK (z)dz (9.23)