Question: 1. Consider the following portfolio optimization problem: where is the expected return vector, is the return covariance matrix, and p is a target level of
1. Consider the following portfolio optimization problem:
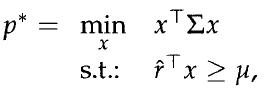
where ![]() is the expected return vector,
is the expected return vector, ![]() is the return covariance matrix, and p is a target level of expected portfolio return. Assume that the random return vector r follows a simplified factor model of the form
is the return covariance matrix, and p is a target level of expected portfolio return. Assume that the random return vector r follows a simplified factor model of the form
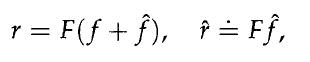
where![]() is a factor loading matrix,
is a factor loading matrix,![]() is given, and
is given, and ![]() is such that
is such that![]()
The above optimization problem is a convex quadratic problem that involves n decision variables. Explain how to cast this problem into an equivalent form that involves only k decision variables. Interpret the reduced problem geometrically. Find a closed-form solution to the problem.
2. Consider the following variation on the previous problem:
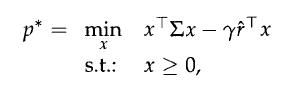
where ![]() is a tradeoff parameter that weights the relevance in the objective of the risk term and of the return term. Due to the presence of the constraint x ≥ 0, this problem does not admit, in general, a closed-form solution.
is a tradeoff parameter that weights the relevance in the objective of the risk term and of the return term. Due to the presence of the constraint x ≥ 0, this problem does not admit, in general, a closed-form solution.
Assume that r is specified according to a factor model of the form![]() where F, / , and / are as in the previous point, and e is an idiosyncratic noise term, which is uncorrelated with
where F, / , and / are as in the previous point, and e is an idiosyncratic noise term, which is uncorrelated with ![]() and such that
and such that ![]()
Suppose we wish to solve the problem using a logarithmic barrier method of the type discussed in Section 12.3.1. Explain how to exploit the factor structure of the returns to improve the numerical performance of the algorithm.
p* = min x st: f x > ,
Step by Step Solution
3.57 Rating (168 Votes )
There are 3 Steps involved in it
Pa... View full answer

Get step-by-step solutions from verified subject matter experts


