We consider a single-period portfolio optimization problem with n assets. We use past samples, consisting of single-period return vectors  where  returns of the assets from period t — 1 to period t. We denote by  the vector of sample averages; it is an estimate of the expected return, based on the past samples.

As a measure of risk, we use the following quantity. Denote by ρt{x) the return at time t (if we had held the position x at that time). Our risk measure is

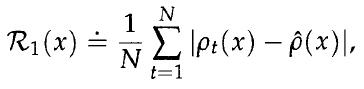
where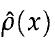is the portfolio's sample average return.

1. Show thatN matrix that you will determine. Is the risk measure R₁ convex?

2. Show how to minimize the risk measure IZi, subject to the condition that the sample average of the portfolio return is greater than a target ]i, using linear programming. Make sure to put the problem in standard form, and define precisely the variables and constraints.
3. Comment on the qualitative difference between the resulting portfolio and one that would use the more classical, variance-based risk measure, given by

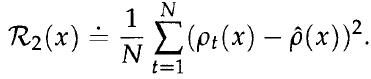
,,N,