Consider a linear least squares problem where the matrix involved is random. Precisely, the residual vector is of the form A()x b, where the

Consider a linear least squares problem where the matrix involved is random. Precisely, the residual vector is of the form A(δ)x – b, where the m x n A matrix is affected by stochastic uncertainty. In particular, assume that

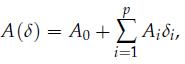
where δ_i, i = 1, . . . , p are i.i.d. random variables with zero mean and variance σ²_i . The standard least-squares objective function ΙΙA(δ)x – bΙΙ²₂ is now random, since it depends on δ. We seek to determine x such that the expected value (with respect to the random variable d) ofis minimized. Is such a problem convex? If yes, to which class does it belong to (LP, LS, QP, etc.)?

p () = Ao + , i=1