The gain of a system is the maximum energy amplification from the input signal to output. Any input signal u(t) having finite energy is mapped by a stable system to an output signal y{t) which also has finite energy. Parseval's identity relates the energy of a signal ω(t) in the time domain to the energy of the same signal in the Fourier domain (see Remark 13.1), that is

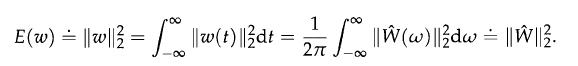
The energy gain of system (13.26) defined as

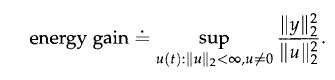
1. Using the above information, prove that, for a stable system,

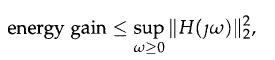
where ΙΙH(jω)ΙΙ₂ is the spectral norm of the transfer matrix of system (15.26), evaluated at s = jω. The (square-root of the) energy gain of the system is also known as the H_∞ - norm, and it is denoted by ΙΙHΙΙ_∞.

2. Assume that system (15.26) is stable, x(0) = 0, and D = 0. Prove  that if there exists such  such that

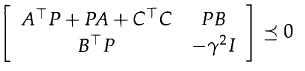
then it holds that

Devise a computational scheme that provides you with the lowest possible upper bound ϒ* on the energy gain of the system.

Define a quadratic function V(x) = x^TPx, and observe that the derivative in time of V, along the trajectories of system (15.26), is

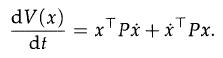
Then show that the LMI condition (15.32) is equivalent to the condition that

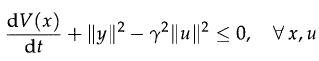
and that this implies in turn that ΙΙHΙΙ_∞ ≤ ϒ

1 E(w) = ||w|| = | ||w(t)||/dt = 2/7 ||(w)||dw = ||W|| .