Consider a continuous-time LTI system x(t) = Ax(t), t ≥ 0, with no input (such a system is said to be autonomous), and output y(t) = Cx. We wish to evaluate the energy contained in the system's output, as measured by the index

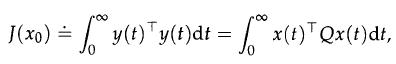
where

1. Show that if the system is stable, then J( xq) 0.

2. Show that if the system is stable and there exists a matrixsuch that 

then it holds that J(x₀) ≤ x₀^TPx₀.

3. Explain how to compute a minimal upper bound on the state energy, for the given initial conditions.

I(xo) = y(t)Ty(t)dt = x(t)Qx(t)dt, 00 0