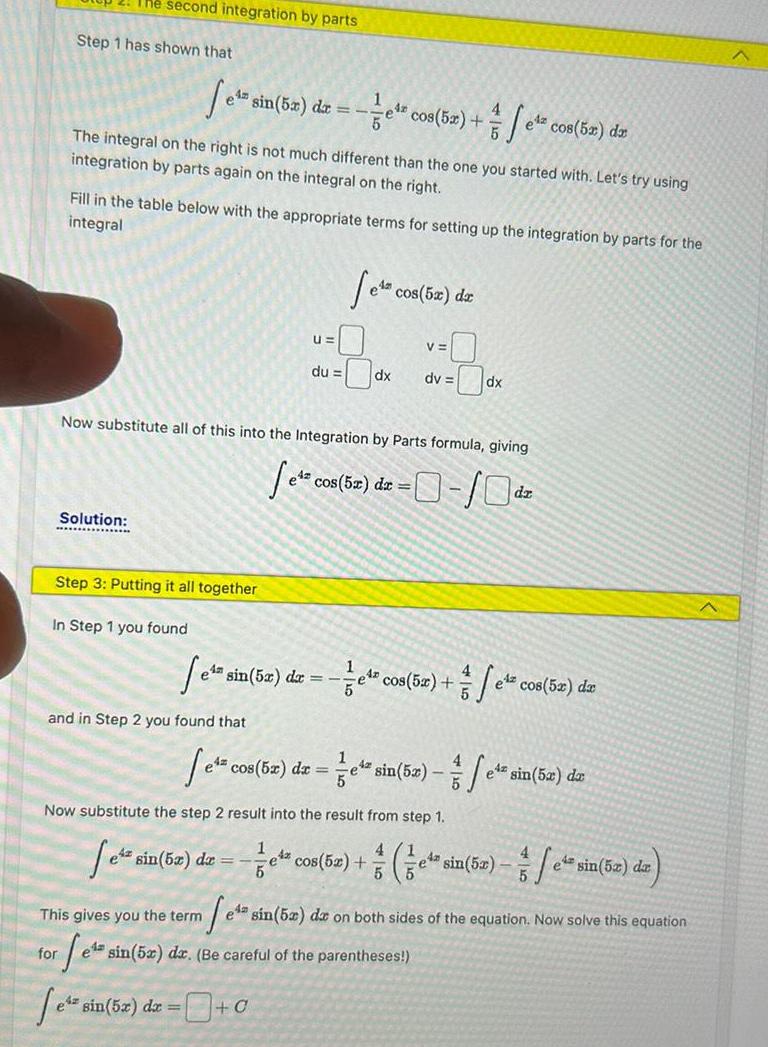
2. The second integration by parts Step 1 has shown that Se sin(5x) dr = cos(5x) + 1 Az fez c cos(5x) dx The integral on the right is not much different than the one you started with. Let's try using integration by parts again on the integral on the right. Fill in the table below with the appropriate terms for setting up the integration by parts for the integral e* cos(5x) dz u= V= =0 du = d dx dv= dx Now substitute all of this into the Integration by Parts formula, giving Se cos(5x) dr= =0-/Odz Solution: Step 3: Putting it all together In Step 1 you found Se sin(5x) dr = cos(5x) + and in Step 2 you found that Setz 1 42 Sec cos(5x) da e cos(5x) dr = e sin(5x)-e* sin(5x) dz 5 Now substitute the step 2 result into the result from step 1. e sin(52) dr = 1 4x 5 4 e sin(5x) dz cos(5x)+(e sin(5)-e This gives you the term neta sin (52) dz on both sides of the equation. Now solve this equation for et sin(5x) dr. (Be careful of the parentheses!) e sin(5x) dr=+0