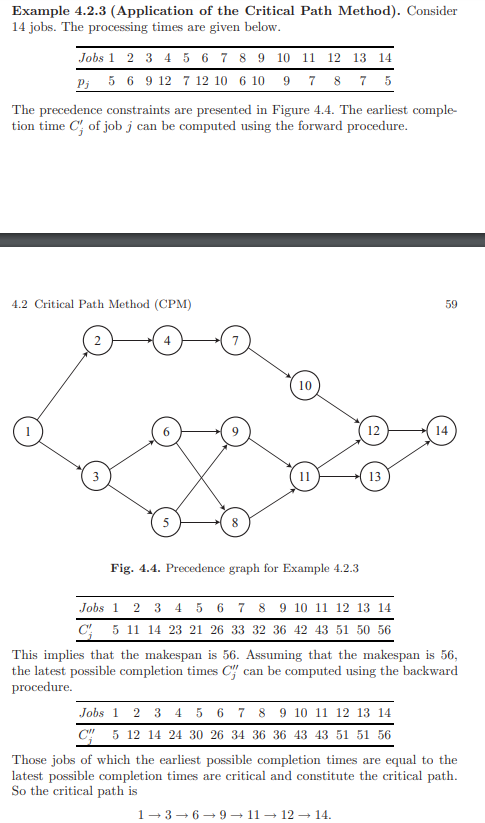
4.1. Consider the job-on-node representation depicted in Example 4.2.3. Transform this job-on-node representation into a job-on-arc representation. Compare the number of nodes and arcs in the first representation with the number of nodes and arcs in the second representation. Can you make any general statement with regard to such a comparison? Example 4.2.3 (Application of the Critical Path Method). Consider 14 jobs. The processing times are given below. The precedence constraints are presented in Figure 4.4. The earliest completion time Cj of job j can be computed using the forward procedure. 4.2 Critical Path Method (CPM) 59 Fig. 4.4. Precedence graph for Example 4.2.3 This implies that the makespan is 56. Assuming that the makespan is 56 , the latest possible completion times Cj can be computed using the backward procedure. Those jobs of which the earliest possible completion times are equal to the latest possible completion times are critical and constitute the critical path. So the critical path is 1369111214