A classification is a form of data analysis where a model or classifier is constructed to predict class labels or types. Data classification is a two-phase process, 1) a learning phase in which the classifier is built and 2) a classifying phase where the determination of the class type of given data is performed. With this project, students will be able to address problems in the two phases of classification, by implementing a basic algorithm to construct a classifier and by determining the class labels of given data tuples.

Problem

Our textbook describes in Section 8.2.1 a basic algorithm for inducing a decision tree from training tuples. The algorithm follows a top-down approach, similar to how decision trees are constructed by algorithms such as ID3, C4.5, and CART.

Part 1

Write a Java program that implements the basic algorithm for inducing a decision tree.

Note the following requirements:

-You are not required to fully implement the algorithm as given in pages 332 –335, but to implement the partition that occurs at the root node, i.e. the generation of the first level after the root. Use the description in Figure 8.3 for the algorithm steps, page 333, and the illustration in Figure 8.5 as a reference of the expected output.

-Consider the splitting attribute to be discrete-valued and use information gain as the attribute selection measure.

-Your implementation should use the training tuples given in Table 8.1, page 338 of the textbook. When run, the program should output the information given in Figure 8.5 (the output does not need to look exactly in the way shown there, but must convey the same meaning).

Part 2

Test the implementation in Part 2 by asking the user to enter a tuple and letting the model determine the class label for the tuple.

REFERENCES

8.2.1 Decision Tree Induction

During the late 1970s and early 1980s, J. Ross Quinlan, a researcher in machine learning, developed a decision tree algorithm known as ID3 (Iterative Dichotomiser). This work expanded on earlier work on concept learning systems, described by E. B. Hunt, J. Marin, and P. T. Stone. Quinlan later presented C4.5 (a successor of ID3), which became a benchmark to which newer supervised learning algorithms are often compared. In 1984, a group of statisticians (L. Breiman, J. Friedman, R. Olshen, and C. Stone) published the book Classification and Regression Trees (CART), which described the generation of binary decision trees. ID3 and CART were invented independently of one another at around the same time, yet follow a similar approach for learning decision trees from training tuples. These two cornerstone algorithms spawned a flurry of work on decision tree induction. ID3, C4.5, and CART adopt a greedy (i.e., nonbacktracking) approach in which decision trees are constructed in a top-down recursive divide-and-conquer manner. Most algorithms for decision tree induction also follow a top-down approach, which starts with a training set of tuples and their associated class labels. The training set is recursively partitioned into smaller subsets as the tree is being built. A basic decision tree algorithm is summarized in Figure 8.3. At first glance, the algorithm may appear long, but fear not! It is quite straightforward. The strategy is as follows. The algorithm is called with three parameters: D, attribute list and Attribute selection method. We refer to D as a data partition. Initially, it is the complete set of training tuples and their associated class labels. The parameter attribute list is a list of attributes describing the tuples. The attribute selection method specifies a heuristic procedure for selecting the attribute that “best” discriminates the given tuples according to class. This procedure employs an attribute selection measure such as information gain or the Gini index. Whether the tree is strictly binary is generally driven by the attribute selection measure. Some attribute selection measures, such as the Gini index, enforce the resulting tree to be binary. Others, like information gain, do not, therein allowing multiway splits (i.e., two or more branches to be grown from a node). The tree starts as a single node, N, representing the training tuples in D (step 1).3

 

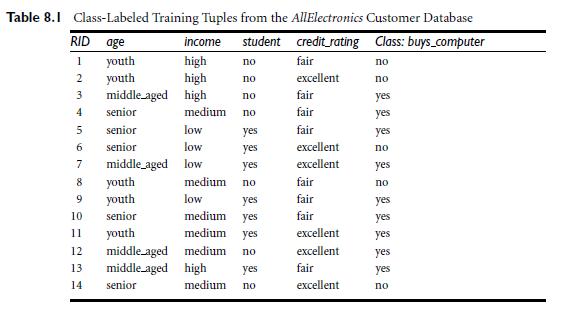
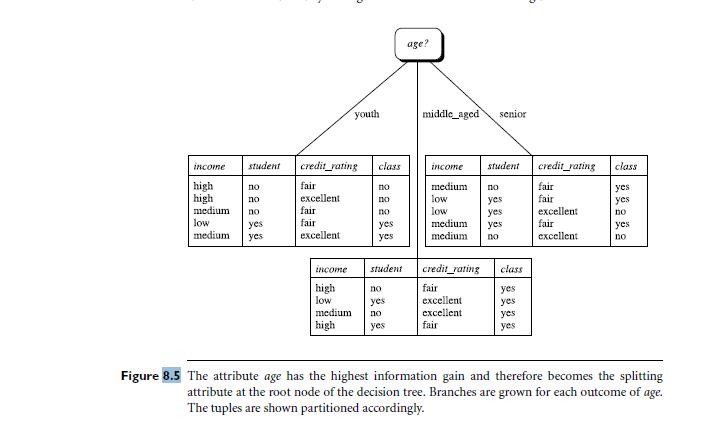
Table 8.1 Class-Labeled Training Tuples from the AllElectronics Customer Database RID age credit rating Class: buys_computer 1 fair excellent fair fair fair 2 3 4 5 6 7 8 9 10 11 12 13. 14 youth youth middle_aged senior senior senior middle youth youth senior youth income student high no high high no medium low low aged low middle-aged middle aged senior yes yes yes medium no low yes medium yes medium yes medium no high yes medium no excellent excellent fair fair fair excellent excellent fair excellent no no yes yes yes no yes no yes yes yes yes yes no Algorithm: Generate_decision_tree. Generate a decision tree from the training tuples of data partition, D. Input: Output: A decision tree. Method: (3) (4) (5) (6) Data partition, D, which is a set of training tuples and their associated class labels; attribute_list, the set of candidate attributes; (1) create a node N; (2) if tuples in D are all of the same class, C, then Attribute_selection method, a procedure to determine the splitting criterion that best partitions the data tuples into individual classes. This criterion consists of a splitting_attribute and, possibly, either a split-point or splitting subset. (11) (12) (7) label node N with splitting_criterion, (8) (13) (14) return N as a leaf node labeled with the class C; if attribute_list is empty then return N as a leaf node labeled with the majority class in D; // majority voting apply Attribute_selection method(D, attribute_list) to find the best splitting_criterion, if splitting attribute is discrete-valued and multiway splits allowed then // not restricted to binary trees (9) attribute_list attribute_list-splitting_attribute; // remove splitting_attribute (10) for each outcome j of splitting_criterion // partition the tuples and grow subtrees for each partition let D; be the set of data tuples in D satisfying outcome j: // a partition if Dj is empty then attach a leaf labeled with the majority class in D to node N; else attach the node returned by Generate_decision_tree(Dj, attribute_list) to node N; endfor (15) return N; Figure 8.3 Basic algorithm for inducing a decision tree from training tuples. student income high high no no medium no low medium yes yes credit_rating fair excellent fair fair excellent income high low youth medium high class no no no yes yes student no yes no yes age? middle aged income student credit_rating medium yes yes low low senior medium yes medium no credit_rating fair excellent excellent fair class yes yes yes yes fair fair excellent fair excellent class yes yes no yes no. Figure 8.5 The attribute age has the highest information gain and therefore becomes the splitting attribute at the root node of the decision tree. Branches are grown for each outcome of age. The tuples are shown partitioned accordingly.