Based on the example problem below, answer this question please: Being a company about to go bankrupt, you can only afford a 2.5 m CSTR. What conversion can you achieve?

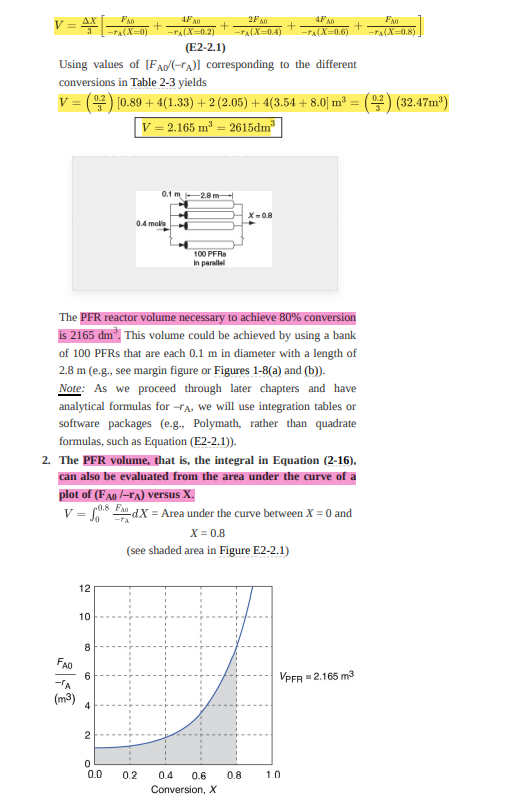
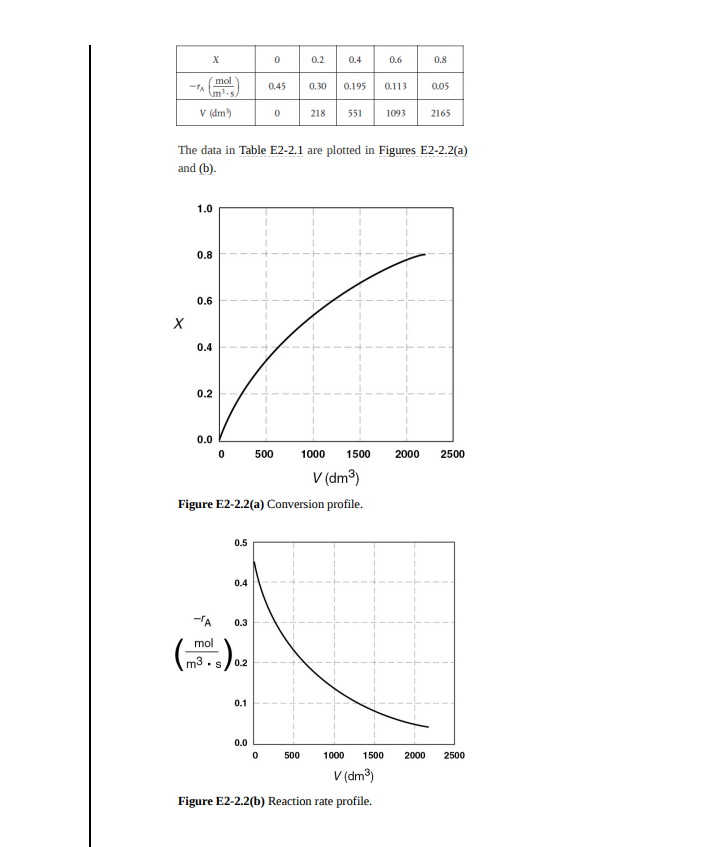
Example 2-2 Sizing a PFR The reaction described by the data in Tables 2-1 and 2- 2 is to be carried out in a PFR. The entering molar flow rate of A is again, Fao = 0.4 mol/s. 1. First, use one of the integration formulas given in Appendix A.4 to determine the PFR reactor volume necessary to achieve 80% conversion. 2. Next, shade the area in Figure 2-26) that would give the PFR volume necessary to achieve 80% conversion. 3. Finally, make a qualitative sketch of the conversion, X, and the rate of reaction, -ra, down the length (volume) of the reactor. Solution We start by repeating rows 1 and 4 of Table 2-2 to produce the results shown in Table 2-3 TABLE 2-3 PROCESSED DATA 2 X 0.0 0.1 0.2 0.4 0.6 0.7 0.8 (Fl-Jim) 0.89 1.08 1.33 2.05 3.54 5.06 8.0 1. (a) Numerically evaluate PFR volume. For the PFR, the differential form of the mole balance is FOX = -r (2-15) Rearranging and integrating gives -0.8 0.8 FM V = Fx108 * = 4.3 FAX (2-16) We shall use the five-point quadrature formula (Equation (A- 23)) given in Appendix A.4 to numerically evaluate Equation (2-16). The five-point formula with a final conversion of 0.8 gives four equal segments between X = 0 and X = 0.8, with a segment length of AX =0,8 = 0.2. The function inside the integral is evaluated at X = 0, X = 0.2, X = 0.4, X = 0.6, and X = 0.8. 4 AX 2FND Fre FA -TAX=0) -TA(X=0.4) 4F AD TAX0.6) -TA(X=0.8) 4F V = 48 AD (- -TAX=0.2) (E2-2.1) Using values of [Fad (ra)] corresponding to the different conversions in Table 2-3 yields V = (93) [0.89 +4(1.33) + 2 (2.05) + 4(3.54 +8.0) m* = (03) (32.47m) V = 2.165 ml = 2615dm 0.1-2.8m X=0.8 0.4 mois 100 PFRS In parallel The PFR reactor volume necessary to achieve 80% conversion is 2165 dm. This volume could be achieved by using a bank of 100 PFRs that are each 0.1 m in diameter with a length of 2.8 m (e.g., see margin figure or Figures 1-8(a) and (b)). Note: As we proceed through later chapters and have analytical formulas forra, we will use integration tables or software packages (e.g., Polymath, rather than quadrate formulas, such as Equation (E2-2.1)). 2. The PFR volume, that is, the integral in Equation (2-16). can also be evaluated from the area under the curve of a plot of (FA0 /-rA) versus X. V = LOS FAX = Area under the curve between X = 0 and 0.8 X = 0.8 (see shaded area in Figure E2-2.1) 12 10 8 FAO 6 VPFR = 2.165 m3 -A (m3) 4 2 0 0.0 02 0.8 10 04 0.6 Conversion, X Figure E2-2.1 Levenspiel PFR plot. PER The area under the curve will give the tubular reactor volume necessary to achieve the specified conversion of A. For 80% conversion, the shaded area is roughly equal to 2165 dm (2.165 m). 3. Sketch the profiles of =rA and X down the length of the reactor. We know that as we proceed down the reactor, the conversion increases as more and more reactant is converted to product. Consequently, as the reactant is consumed, the concentration of reactant decreases, as does the rate of disappearance of A for isothermal reactions. 1. For X = 0.2, we calculate the corresponding reactor volume using Simpson's rule (given in Appendix A.4 as Equation (A-21)) with increment =X = 0.1 and the data in rows 1 and 4 in Table 2-2. FR AFM + (X-0) FAD (X-02) + 3 (E2 - 2.2) mol V = F, S.22 4x (X-0.1) 10.89 + 4 (1.08) + 1.33))m= 4(6.54m") = 0.218m = 218m? 218 m This volume (218 m) is the volume at which X = 0.2. From Table 2-2, we see the corresponding rate of reaction at X = 0.2 is A = 0.3- Therefore at X = 0.2, then - TA = 0.3 mol/ ms and V = 218 dm". 2. For X = 0.4, we can again use Table 2-3 and Simpson's rule with AX = 0.2 to find the reactor volume necessary for a conversion of 40%. V = 42 ( 92 (0.89 + 4 (1.33)] +2.05 ) m = 0.551m = 551 dm From Table 2-2 we see that at X = 0.4, - A = 0.195 mol m.s and V = 551 dm We can continue in this manner to arrive at Table E2-2.1. AFN FA -A(X) -> (X-02) Fro - (X-0.4) TABLE E2-2.1 CONVERSION AND REACTION RATE PROFILES 0 0.2 0.4 0.6 0.8 mol -TA 0.45 0.30 0.195 0.113 0.05 v (dm) 0 218 551 1093 2165 The data in Table E2-2.1 are plotted in Figures E2-2.2(a) and (b). 1.0 0.8 0.6 0.4 0.2 0.0 0 500 1000 1500 2000 2500 V (dm) Figure E2-2.2(a) Conversion profile. 0.5 0.4 -TA 0.3 mol m3 .S O's) 0.2 0.1 0.0 0 2000 2500 500 1000 1500 V(dm) Figure E2-2.2(b) Reaction rate profile