BASED ON THE FOLLOWING PROBLEM please show How would your answers change if the two CSTRs (one 0.82 m and the other 3.2 m ) were placed in PARALLEL with the flow, F , divided equally between the reactors?

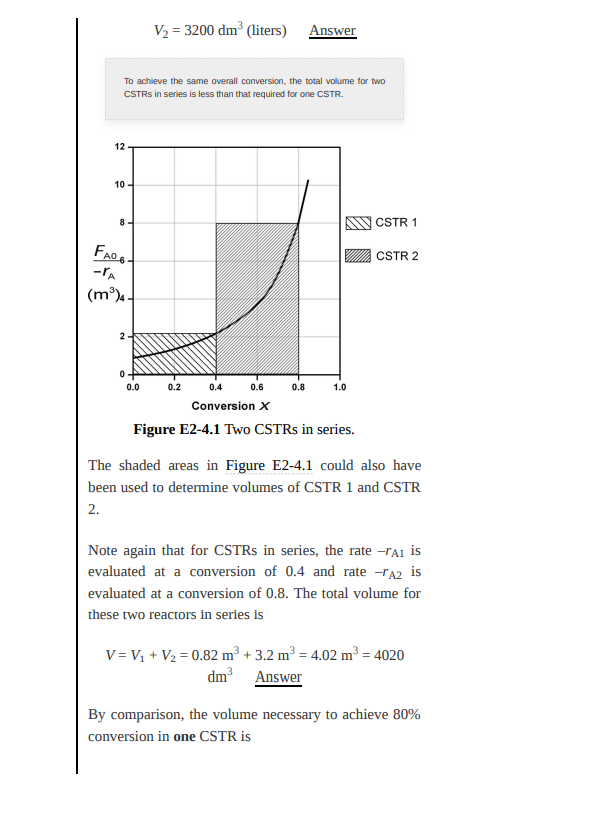
Example 2-4 Comparing Volumes for CSTRs in Series For the two CSTRs in series, 40% conversion is achieved in the first reactor. What is the volume of each of the two reactors necessary to achieve 80% overall conversion of the entering species A? (See Table 2-3.) TABLE 2-3 PROCESSED DATA 2 0.0 0.1 0.2 0.4 0.6 0.7 0.8 (ForJ(m) 0.89 1.08 1.33 2.05 3.54 5.06 8.0 Solution For Reactor 1, we observe from either Table 2-3 or Figure 2-2(b) that when X = 0.4, then FAO -TAI -)x=0.4=2.05m Then, using Equation (2-13) Vi=4 )4X1=CM)0.4X1=(2.05)(0.4)=0.82m2=820dm3 G -, = V1 = 820 dm (liters) Answer For Reactor 2, when X2 0.8, then CE )x=. FAO - x=0.8=8. Om Using Equation (2-24) FA V2=C)(X, X1) (2-24) V2 = (8.0 m)(0.8 -0.4) = 3.2 m = 3200 dm3 m V2 = 3200 dm (liters) Answer To achieve the same overall conversion, the total volume for two CSTRs in series is less than that required for one CSTR. 12 10 - 8- M CSTR 1 FAROL CSTR 2 -TA (m) - 2 0 0.0 0.2 0.4 0.6 0.8 1.0 Conversion X Figure E2-4.1 Two CSTRs in series. The shaded areas in Figure E2-4.1 could also have been used to determine volumes of CSTR 1 and CSTR 2. Note again that for CSTRs in series, the rate - Ai is evaluated at a conversion of 0.4 and rate - A2 is evaluated at a conversion of 0.8. The total volume for these two reactors in series is V = V1 + V2 = 0.82 m + 3.2 m = 4.02 m = 4020 dm Answer By comparison, the volume necessary to achieve 80% conversion in one CSTR is y=() X -) X=(8.0) (0.8)=6.4m=6400dm? Answer FAO TAL We need only - A = f(x) and Fap to size reactors. Notice in Example 2-4 that the sum of the two CSTR reactor volumes (4.02 m) in series is less than the volume of one CSTR (6.4 m) to achieve the same overall conversion. Analysis: When we have reactors in series, we can speed our analysis and calculations by defining an overall conversion at a point in the series, rather than the conversion of each individual reactor. In this example, we saw that 40% was achieved at point 1, the exit to the first reactor, and that a total of 80% conversion was achieved by the time we exit the second reactor. Using two CSTRs in series will give a smaller total volume than one CSTR to achieve the same conversion