calulus 3 :

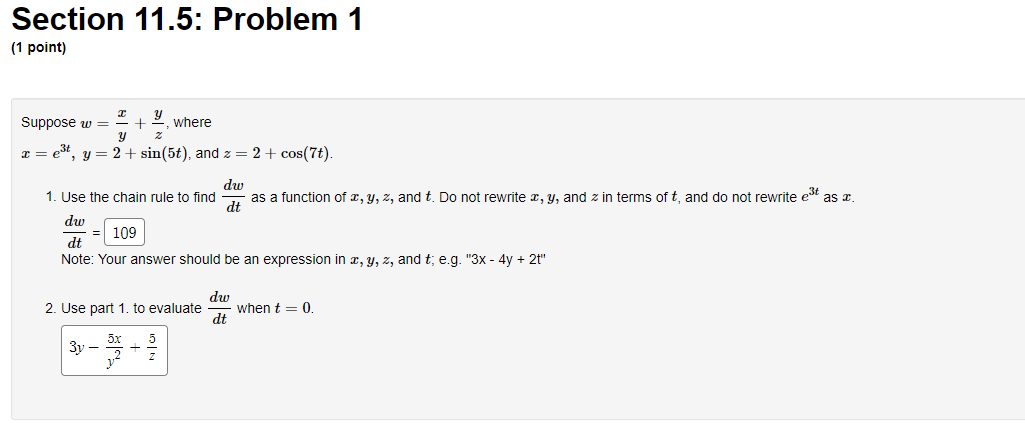
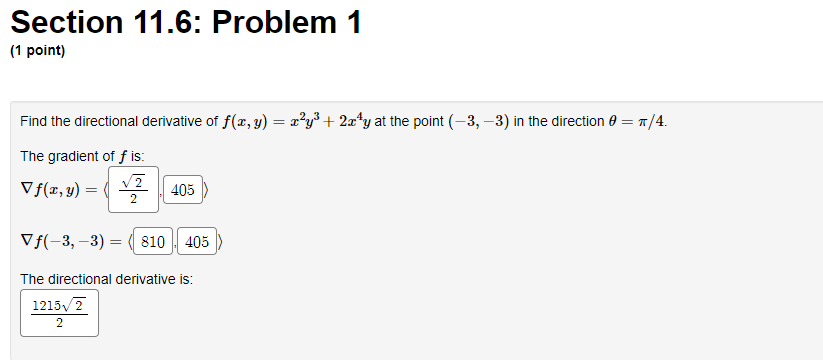
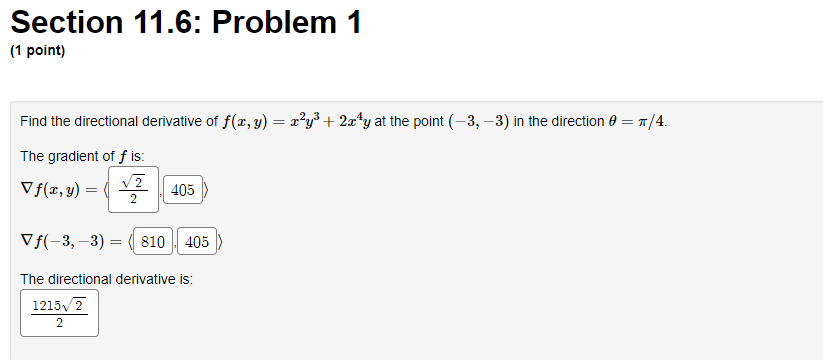
Section 11.5: Problem 1 (1 point) Suppose w = - + - 2, where y Z @ =e", y = 2 + sin(5t), and z = 2 + cos(7t). dw 1. Use the chain rule to find dt as a function of I, y, z, and t. Do not rewrite x, y, and z in terms of t, and do not rewrite ed as r. dw 109 dt Note: Your answer should be an expression in a, y, z, and t; e.g. "3x - 4y + 2t" dw 2. Use part 1. to evaluate when t = 0. dt 3v OXSection 11.5: Problem 2 (1 point) Suppose z = x sin(y) , x = 482 - t2, y = -6st. A. Use the chain rule to find and as functions of c, y, s and t. Oz B. Find the numerical values of and DE when (s, t) = (5, 4). DS (5, 4) Oz Of (5, 4) =Section 11.5: Problem 3 (1 point) Use the chain rule to find s and of, where 7s z = etan(y), x = 2s + 2t, y= 3t First the pieces: 2 Dy 2 3t 75 = dy = 31 dy 75 THE 3t And putting it all together: Oz Ox Oz oz Dy and " = Oz dy = + dy Us + dy Ot\fSection 11.5: Problem 7 (1 point) Consider the surface F(x, y, 2) = 2 2 + sin (162) -1 = 0. Find the following partial derivatives Dz 3x 2-8 542.87Section 11.5: Problem 9 (1 point) In a simple electric circuit, Ohm's law states that V = IR, where V is the voltage in Volts, I is the current in Amperes, and R is the resistance in Ohms. Assume that, as the battery wears out, the voltage decreases at 0.02 Volts per second and, as the resistor heats up, the resistance is increasing at 0.02 Ohms per second. When the resistance is 100 Ohms and the current is 0.04 Amperes, at what rate is the current changing? 0.000208 Amperes per secondSection 11.6: Problem 1 (1 point) Find the directional derivative of f(x, y) = x y* + 2xy at the point (-3, -3) in the direction 0 = 1 /4. The gradient of f is: Vf (x, y) = V 2 2 405 = (8-'E-)fA 810 405 The directional derivative is: 1215\\ 2 2Section 11.6: Problem 2 (1 point) Consider the function f(x, y, 2) = xy + yz + x23 Find the gradient of f: Find the gradient of f at the point (1, -4, -5). -129 26 115 Find the rate of change of the function f at the point (1, -4, -5) in the direction u = (5/v38, -2/V38,3/v38). 176: 38 19Section 11.6: Problem 5 (1 point) Find the maximum rate of change of f(x, y, >) = = + ~ at the point (2, -2, -5) and the direction in which it occurs. Maximum rate of change: 625 + 25 + 4 625 Direction in which it occurs