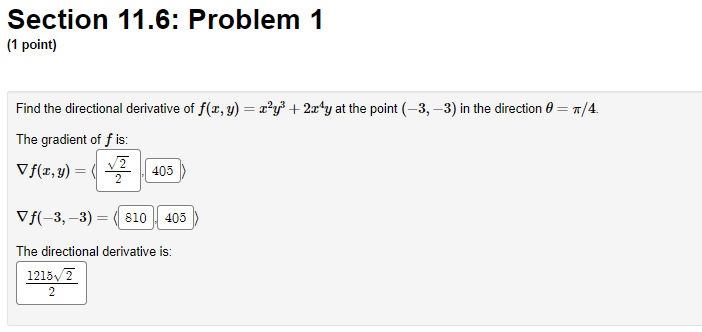
Question: Calculus 3 : > Section 11.6: Problem 1 (1 point) Find the directional derivative of f(x, y) = xy* + 2xly at the point (-3,
Calculus 3 :
>







![Problem 18 {1 point] 140 The temperature at anyI paint in the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6681e91a96fe5_8506681e91a847c8.jpg)

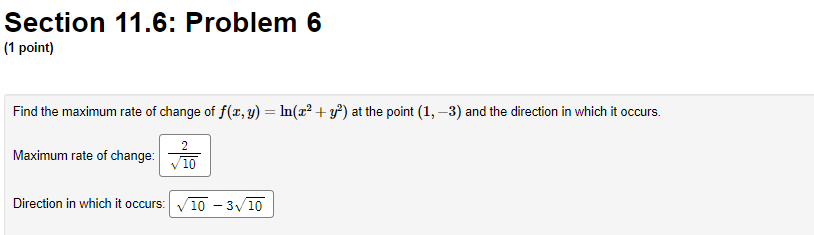
Section 11.6: Problem 1 (1 point) Find the directional derivative of f(x, y) = xy* + 2xly at the point (-3, -3) in the direction 0 = 7/4. The gradient of f is: = (6 'I)/A V/2 2 405 Vf(-3, -3) = 810 405 The directional derivative is: 1215: 2 2Section 11.6: Problem 12 (1 point) Consider the surface z - 10 = ce' cos z. Find an equation of the tangent plane to this surface at (-10, 0, 0). X - 7+ 10 =0 Find a vector equation for the normal line to the surface at (-10, 0, 0). r(t ) = Section 11.6: Problem 18 {1 point] 140 The temperature at anyI paint in the plane is given by T[z, y} = W. 3 {a} What shape are the level curves of T? on. hyperbolas @ B. circles Q C. parabolas O D. lines 0 E. ellipses O F. none at the above (h) At what point on the plane is it hottest? {[011] What is the maximum temperature? [c] Find the direction ufthe greatest increase in temperature at the paint (1, 3]_ What is the value at this maximum rate of change, that is, the maximum value at the directional derivative at [1,3)? 7131 m {d} Find the direction of the greatest decrease in temperature at the point (1: 3). What is the value at this most negative rate of change, that is, the minimum value of the directional derivative at (1I 3]'? Section 11.6: Problem 2 {1 point] Consider the fundidn m, y, z) = my + p.33 + 12'. Find The gradient at f: I C} C]? Find The gradient at f at the point (1, 4, 5}.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


